安徽省阜阳市阜南县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下面的图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列函数中，y随x的增大而减小的是（）

A、 $y = \frac{1}{2} x$ B、 $y = \frac{2}{x}$ C、 $y = - \frac{1}{2} x$ D、 $y = - \frac{2}{x}$

查看试题解析
3. 下列命题：①垂直于弦的直径平分弦，并且平分弦所对的两条弧；②在同圆或等圆中相等的圆心角所对的弧相等；③在同圆或等圆中如果两条弦相等，那么它们所对的圆心角相等；④圆内接四边形的对角互补．其中正确的命题共有（）

A、 $4$ 个 B、 $3$ 个 C、 $2$ 个 D、 $1$ 个

查看试题解析
4. 已知在 $Rt △ A B C$ 中， $∠ C = 90^{°} ， A B = 3 ， B C = 2$ ，那么 $\tan B$ 的值等于（）

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{5}}{3}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
5. 在同一平面直角坐标系中，函数y＝kx+1（k≠0）和 $y = \frac{k}{x}$ （k≠0）的图象大致是（）

A、 B、 C、 D、

查看试题解析
6. 如图，已知∠1＝∠2，添加下列条件后，仍无法判定△ABC∽△ADE的是（）

A、 $\frac{A B}{A D}$ ＝ $\frac{A C}{A E}$ B、∠B＝∠D C、∠C＝∠AED D、 $\frac{A B}{A D}$ ＝ $\frac{B C}{D E}$

查看试题解析
7. 用min{a ， b}表示a ， b两数中的最小数，若函数 $y = \min {x^{2} + 1 ， 1 - x^{2}}$ ，则y的图象为（）

A、 B、 C、 D、

查看试题解析
8. 如图，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数 $y = \frac{k}{x}$ 在第一象限内的图像经过点D，交BC于点E，若AB=4，CE=2BE， $\tan ∠ A O D = \frac{3}{4}$ ．则k的值为（）

A、3 B、 $2 \sqrt{3}$ C、6 D、12

查看试题解析
9. 如图，二次函数y＝ax²＋bx＋c的图象经过点A(﹣3，0)，其对称轴为直线x＝﹣1，有下列结论：①abc＜0；②a＋b＋c＜0；③2a－b＝0；④4ac﹣b²＞0；⑤若P(﹣5，y₁)，Q(m，y₂)是抛物线上两点，且y₁＞y₂ ，则实数m的取值范围是﹣5＜m＜3．其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图， $R t △ A B C$ 中， $A B = B C$ ，点D是AB的中点，连接CD ，过点B作 $B G ⊥ C D$ ，分别交CD ， CA于点E ， F ，与过点A且垂直于AB的直线相交于点G ，下列结论正确的是（）

A、 $E F = G F$ B、 $∠ A D F = ∠ C D B$ C、 $A F = \frac{\sqrt{2}}{2}$ AB D、 $S_{△ A B C} = 5 S_{△ B D F}$

查看试题解析

二、填空题

11. 若关于x的一元二次方程x²+mx+2n=0有一个根是2，则m+n= ．

查看试题解析
12. 如图，圆锥的表面展开图由一扇形和一个圆组成，已知圆的面积为100π，扇形的圆心角为120°，这个扇形的面积为．

查看试题解析
13. 点A ， B ， C ， D都在 $⊙ O$ 上， $\overset{⌢}{A B} = \overset{⌢}{A C}$ ，D为 $⊙ O$ 上的一点， $∠ A B C = ∠ O D C = 67.5 °$ ， $CO$ 的延长线交AB于点P ，若 $C D = 2$ ，则 $B P =$ ．

查看试题解析
14. 抛物线 $y = a x^{2} - x + 1 (a \neq 0)$ 与线段 $A B$ 有两个不同的交点，已知 $A (- 1 ， 0)$ ， $B (1 ， 1)$ ，则 $a$ 的取值范围是．

查看试题解析

三、解答题

15. 计算： $| - \frac{1}{2} | + \sqrt{9} - {(- 2)}^{- 2} - {(3.14 - π)}^{0} - 4 \cos 30 ° + | 2 - \sqrt{12} |$ ．

查看试题解析
16. 先化简，后求值： $（ \frac{1}{a - 1} - \frac{1}{a + 1} ） \div \frac{4 + 2 a}{a^{2} - 1}$ ，其中 $a = - 2 + \sqrt{2}$

查看试题解析
17. 如图，在边长为1的正方形网格中，△ABC的顶点均在格点上，把△ABC绕点C逆时针旋转90°后得到△A₁B₁C．

(1)、画出△A₁B₁C，；

(2)、求在旋转过程中，CA所扫过的面积．

查看试题解析
18. 如图，一次函数 $y = x + 1$ 与反比例函数 $y = \frac{k}{x}$ 的图像相交于点 $A (2 ， 3)$ 和点 $B$ ．

(1)、求反比例函数的解析式；

(2)、过点 $B$ 作 $B C ⊥ x$ 轴于 $C$ ，求 $S_{△ A B C}$ ；

(3)、是否在 $y$ 轴上存在一点 $D$ ，使得 $B D + C D$ 的值最小，并求出 $D$ 坐标．

查看试题解析
19. 中国“蛟龙”号深潜器目前最大深潜极限为 $7062.68$ 米，某天该深潜器在海面下 $1800$ 米处作业（如图），测得正前方海底沉船 $C$ 的俯角为 $45^{\circ}$ ，该深潜器在同一深度向正前方直线航行 $2000$ 米到 $B$ 点，此时测得海底沉船 $C$ 的俯角为 $60^{\circ}$ ．沉船 $C$ 是否在“蛟龙”号深潜极限范围内？并说明理由
$(\sqrt{2} \approx 1.414 ， \sqrt{3} \approx 1.732)$

查看试题解析
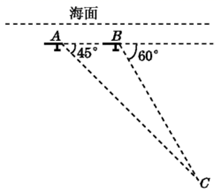20. 如图，⊙O是△ABC的外接圆，BC为⊙O的直径，点E为△ABC的内心，连接AE并延长交⊙O于D点，连接BE ．

(1)、求证：DB＝DE；

(2)、若过C点的切线与BD的延长线交于点F ，已知DE $= 3 \sqrt{2}$ ，求弧DC、线段DF、CF围成的阴影部分面积．

查看试题解析
21. 已知：如图，在△ABC中，点D在边BC上，AE∥BC ， BE与AD、AC分别相交于点F、G ， $A F^{2} = F G \cdot F E$ ．

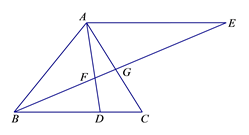(1)、求证：△CAD∽△CBG；

(2)、联结DG ，求证： $D G \cdot A E = A B \cdot A G$ ．

查看试题解析
22. 某商场试销一种成本为每件 $60$ 元的服装，规定试销期间销售单价不低于成本单价，且每件的利润率不得高于 $45 %$ ，经试销发现，销售量 $y$ （件）与销售单价 $x$ （元）符合一次函数 $y = - x + 120$

(1)、若该服装获得利润为 $w$ （元），试写出利润 $w$ 与销售单价 $x$ 之间的关系式；销售单价定为多少时，商场可获得利润最大，最大利润是多少元？

(2)、若该商场获得利润不低于 $500$ 元，试确定销售单价 $x$ 的取值范围．

查看试题解析
23. 在 $△ A B C$ 中， $A B = 5$ ， $B C = 7$ ， $A C = 3$ ．

(1)、求证： $∠ A = 120 °$ ．

(2)、在（1）的基础上，请画一个三边长均为整数，且一个角的度数也是整数的非直角三角形．

(3)、以 $B C$ 为边向下侧作一个等边 $△ B C D$ ，连接 $A D$ ，那么 $A D$ 的长是多少?

查看试题解析