安徽省阜阳市2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，在 $R t △ A B C$ 中， $∠ A = 90 °$ ， $\sin B = \frac{1}{3}$ ， $A C = 2$ ，则 $B C$ 的长为（）

A、2 B、4 C、6 D、8

查看试题解析
2. 反比例函数y＝ $\frac{k - 1}{x}$ 的图象在每一象限内，y随x的增大而减小，则k的取值范围是（）

A、k $>$ 1 B、k $<$ 1 C、k＝1 D、k≠1

查看试题解析
3. 已知抛物线 $y = x^{2} - x - 1$ 与x轴的一个交点为 $(m ， 0)$ ，则代数式 $m^{2} - m + 2020$ 的值为（）

A、2018 B、2019 C、2020 D、2021

查看试题解析
4. 如图，D是 $△ A B C$ 边 $A B$ 延长线上一点，添加一个条件后，仍然不能使 $△ A C D ∽ △ A B C$ 的是（）

A、 $∠ A C B = ∠ D$ B、 $∠ A C D = ∠ A B C$ C、 $\frac{C D}{B C} = \frac{A D}{A C}$ D、 $\frac{A C}{A B} = \frac{A D}{A C}$

查看试题解析
5. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，那么一次函数 $y = a x + b c$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
6. 如图，小树AB在路灯O的照射下形成投影BC．若树高AB=2m，树影BC=3m，树与路灯的水平距离BP=4.5m．则路灯的高度OP为（）

A、3m B、4m C、4.5m D、5m

查看试题解析
7. 已知二次函数 $y = - {(x - 2)}^{2} + 3$ ，且 $- 1 \leq x \leq 1$ ，下列说法正确的是（）

A、当 $x = 2$ 时，函数有最大值3 B、当 $x = - 1$ 时，函数有最大值－6 C、函数 $y$ 的取值范围是 $2 \leq y \leq 3$ D、函数 $y$ 的取值范围是 $- 6 \leq y \leq 2$

查看试题解析
8. 如图， $A B$ 是斜靠在墙上的长梯， $A B$ 与地面夹角为 $α$ ，当梯顶 $A$ 下滑1米到 $A^{'}$ 时，梯脚 $B$ 滑到 $B^{'}$ ， $A^{'} B^{'}$ 与地面的夹角为 $β$ ，若 $\tan α = \frac{4}{3}$ ， $B B^{'} = 1$ 米，则 $\cos β =$ （）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{2}{5}$

查看试题解析
9. 如图，在平面直角坐标系中，函数 $y = \frac{3}{x}$ $(x > 0)$ 与 $y = x - 1$ 的图象交于点 $P (a ， b)$ ，则代数式 $\frac{1}{a} - \frac{1}{b}$ 的值为（）

A、 $- \frac{1}{4}$ B、 $\frac{1}{4}$ C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
10. 如图，正方形 $A B C D$ 的边长为6，点 $E$ 是 $B C$ 的中点，连接 $A E$ 与对角线 $B D$ 交于点 $G$ ，连接 $C G$ 并延长，交 $A B$ 于点 $F$ ，连接 $D E$ 交 $C F$ 于点 $H$ ，连接 $A H$ ．以下结论：① $∠ D E C = ∠ A E B$ ；② $C F ⊥ D E$ ；③ $A F = B F$ ；④ $\frac{C H}{H F} = \frac{2}{3}$ ，其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 将抛物线 $y = 2 {(x - 1)}^{2}$ 向左平移3个单位，向下平移1个单位后所得到的新抛物线的表达式为．

查看试题解析
12. $Δ A B C$ 中，若 ${(\sin A - \frac{1}{2})}^{2} + | \frac{\sqrt{3}}{2} - \cos B | = 0$ ，则 $∠ C =$ .

查看试题解析
13. 如图，直线 $A B$ 过原点分别交反比例函数 $y = \frac{6}{x}$ ，于A．B，过点A作 $A C ⊥ x$ 轴，垂足为C，则△ $A B C$ 的面积为．

查看试题解析
14. 如图，在 $Δ A B C$ 中，点 $A_{1} ， B_{1} ， C_{1}$ 分别是 $A C ， B C ， A B$ 的中点，连接 $A_{1} C_{1} ， A_{1} B_{1}$ ，四边形 $A_{1} B_{1} B C_{1}$ 的面积记作 $S_{1}$ ；点 $A_{2} ， B_{2} ， C_{2}$ 分别是 $A_{1} C ， B_{1} C ， A_{1} B_{1}$ 的中点，连接 $A_{2} C_{2} ， A_{2} B_{2}$ ，四边形 $A_{2} B_{2} B_{1} C_{2}$ 的面积记作 $S_{2}$ …，按此规律进行下去，若 $S_{Δ A B C} = a$ ，则 $S_{3} =$ ； $S_{n} =$ ．（ $n$ 为正整数）

查看试题解析

三、解答题

15. 如图，由若干个边长为1的小正方形组成的网格中，已知格点线段 $A B$ （端点是网格线的交点）和格点 $O$ ．

(1)、以点 $O$ 为位似中心，画出线段 $A B$ 的位似图形线段 $A_{1} B_{1}$ ，使线段 $A_{1} B_{1}$ 与线段 $A B$ 的相似比为2；

(2)、以点 $A_{1}$ 为旋转中心，画出线段 $A_{1} B_{1}$ 绕点 $A_{1}$ 顺时针旋转90°得到的线段 $A_{1} B_{2}$ ．

查看试题解析
16. 如图，点 $E$ 是平行四边形 $A B C D$ 的边 $A B$ 的中点，连接 $D E$ 交对角线 $A C$ 于点 $F$ ，若 $Δ A E F$ 的面积为1，求平行四边形 $A B C D$ 的面积．

查看试题解析
17. 已知抛物线 $y = a x^{2} + k x - k + 2$ 可由抛物线 $y = - 2 x^{2}$ 平移得到，且经过点 $(- 4 ， - 10)$ ．

(1)、确定 $a ， k$ 的值；

(2)、试确定该抛物线的顶点坐标．

查看试题解析
18. 如图所示，小亮在大楼 $A D$ 的观光电梯中的 $E$ 点测得大楼 $B C$ 楼底 $C$ 点的俯角为60°，此时他距地面的高度 $A E$ 为21米，电梯再上升9米到达 $D$ 点，此时测得大楼 $B C$ 楼顶 $B$ 点的仰角为45°，求大楼 $B C$ 的高度．（结果保留根号）

查看试题解析
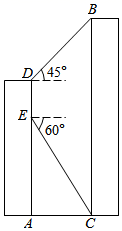19. 对于一个函数给出如下定义：对于函数 $y$ ，若当 $a \leq x \leq b$ ，函数值 $y$ 满足 $m \leq y \leq n$ ，且满足 $n - m = k (b - a)$ ，则称引函数为“ $k$ 属和合函数”．例如：正比例函数 $y = - 2 x$ ，当 $1 \leq x \leq 3$ 时， $- 6 \leq y \leq - 2$ ，则 $- 2 - (- 6) = k (3 - 1)$ ，解得： $k = 2$ ，所以函数 $y = - 2 x$ 为“2属和合函数”．

(1)、一次函数 $y = a x - 1 (a < 0 ， 1 \leq x \leq 3)$ 为“1属和合函数”，求 $a$ 的值；

(2)、反比例函数 $y = \frac{k}{x} (k > 0 ， a \leq x \leq b ，且 0 < a < b)$ 是“ $k$ 属和合函数”，且 $a + b = \sqrt{2020}$ ，请求出 $a^{2} + b^{2}$ 的值．

查看试题解析
20. 从三角形（不是等腰三角形）一个顶点引一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

(1)、如图1，在 $△ A B C$ 中， $∠ A = 48 °$ ， $C D$ 是 $△ A B C$ 的完美分割线，且 $A D = C D$ ，求 $∠ A C B$ 的度数．

(2)、如图2，在 $△ A B C$ 中， $A C = 2$ ， $B C = \sqrt{2}$ ， $C D$ 是 $△ A B C$ 的完美分割线，且 $△ A C D$ 是以 $C D$ 为底边的等腰三角形，找出 $C D$ 与 $B D$ 的关系．

查看试题解析
21. 如图，一艘渔船正以 $\frac{32 \sqrt{3}}{3}$ 海里/小时的速度由西向东赶鱼群，在A处看小岛C在船北偏东60°，60分钟后，渔船行至B处，此时看见小岛C在船的北偏东30°．

(1)、求小岛C到航线AB的距离．

(2)、已知以小岛C为中心周围20海里内为我军导弹部队军事演习的着弹危险区，问这艘渔船继续向东追赶鱼群，是否有进入危险区的可能？若渔船进去危险区，那么经过多少分钟可穿过危险区？

查看试题解析
22. 如图，抛物线 $y = a x^{2} + b x + 2 (a \neq 0)$ 与 $x$ 轴交于 $A (- 1 ， 0) ， B (3 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ．

(1)、求该抛物线的表达式；

(2)、若点 $D$ 是抛物线上第一象限内的一动点，设点 $D$ 的横坐标为 $m$ ，连接 $C D ， B D ， B C ， A C$ ，当 $Δ B C D$ 的面积等于 $Δ A O C$ 面积的2倍时，求 $m$ 的值．

查看试题解析
23. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 ° ， A C = 5 c m ， ∠ B A C = 60 °$ ，动点 $M$ 从点 $B$ 出发，在 $B A$ 边上以每秒 $2 c m$ 的速度向点 $A$ 匀速运动，同时动点 $N$ 从点 $C$ 出发，在 $C B$ 边上以每秒 $\sqrt{3} c m$ 的速度向点 $B$ 匀速运动，设运动时间为 $t$ 秒（ $0 \leq t \leq 5$ ），连接 $M N$ ．

(1)、若 $Δ M B N$ 与 $Δ A B C$ 相似，求 $t$ 的值；

(2)、当 $t$ 为何值时，四边形 $A C N M$ 的面积最小？并求出最小值．

查看试题解析