安徽省滁州市天长市2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，直线 $l_{1} // l_{2} // l_{3}$ ，直线 $A C$ 和 $D F$ 被 $l_{1} ， l_{2} ， l_{3}$ 所截， $A B = 5$ ， $A C = 11$ ， $E F = 4$ ，则 $D E$ 的长为（）

A、2 B、3 C、4 D、 $\frac{10}{3}$

查看试题解析
3. 如图，在△ABC中，∠ACB＝90°，D是AB的中点，若CD＝5，AC＝8，则tanA＝（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
4. 把函数 $y = {(x - 1)}^{2} + 2$ 的图象向右平移1个单位长度，平移后的图象的函数解析式为（）

A、 $y = {(x - 2)}^{2} + 2$ B、 $y = x^{2} + 2$ C、 $y = {(x - 1)}^{2}$ D、 $y = {(x - 1)}^{2} + 3$

查看试题解析
5. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点E ， $B E = 1$ ， $C D = 6$ ，则 $A E$ 的长度为（）

A、10 B、9 C、5 D、4

查看试题解析
6. 若双曲线 $y = \frac{k}{x}$ （ $k < 0$ ），经过点 $A (- 1 ， y_{1})$ ， $B (- 3 ， y_{2})$ ，则 $y_{1}$ 与 $y_{2}$ 的大小关系为（）

A、 $y_{1} < y_{2}$ B、 $y_{1} > y_{2}$ C、 $y_{1} = y_{2}$ D、无法比较 $y_{1}$ 与 $y_{2}$ 的大小

查看试题解析
7. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”.如图，P为 $A B$ 的黄金分割点（ $A P > B P$ ），如果 $A B$ 的长度为 $10 c m$ ，那么较短线段 $B P$ 的长度为（）

A、 $(5 + \sqrt{5}) c m$ B、 $(10 - \sqrt{5}) c m$ C、 $(5 \sqrt{5} - 5) c m$ D、 $(15 - 5 \sqrt{5}) c m$

查看试题解析
8. 河北省赵县的赵州桥的桥拱是近似的抛物线形，建立如图所示的平面直角坐标系，其函数的关系式为y=﹣ $\frac{1}{25}$ x² ，当水面离桥拱顶的高度DO是4m时，这时水面宽度AB为（　　）

A、﹣20m B、10m C、20m D、﹣10m

查看试题解析
9. 如图，已知 $△ A B C$ ， $△ D C E$ ， $△ F E G$ ， $△ H G I$ 是四个全等的等腰三角形，底边 $B C$ ， $C E$ ， $E G$ ， $G I$ 在同一直线上，且 $A B = 4$ ， $B C = 2$ ，连接 $A I$ 交 $F G$ 于点Q ，则 $Q I$ 的值为（）

A、4 B、 $\frac{10}{3}$ C、3 D、 $\frac{8}{3}$

查看试题解析
10. 如图，正方形ABCD和正方形EFGH的对角线BD ， EG都在直线l上，将正方形ABCD沿着直线l从点D与点E重合开始向右平移，直到点B与点G重合为止，设点D平移的距离为x ， $A B = \sqrt{2}$ ， $EH = 2 \sqrt{2}$ ，两个正方形重合部分的面积为S ，则S关于x的函数图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过 $(- 2 ， 4)$ ，则k的值为．

查看试题解析
12. 若 $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ ，根据比例的性质，则 $\frac{a + b + c}{c} =$ ．

查看试题解析
13. 如图，在 $⊙ O$ 中， $A B$ ， $A C$ 是弦，O在 $∠ B A C$ 的内部， $∠ A B O = 25 °$ ， $∠ A C O = 35 °$ ，则 $∠ B O C =$ ．

查看试题解析
14. 如图，在矩形 $A B C D$ 中， $A B = 2$ ， $B C = 4$ ，点M ， N分别在边 $A D$ 和 $B C$ 上.沿 $M N$ 折叠四边形 $A B C D$ ，使点A ， B分别落在 $A_{1}$ ， $B_{1}$ 处，得四边形 $A_{1} B_{1} M N$ ，其中点 $B_{1}$ 在 $D C$ 上，过点M作 $M E ⊥ B C$ 于点E.连接 $B B_{1}$ ．（1） $\frac{M N}{B B_{1}}$ 的值为；（2）当 $B_{1}$ 为 $D C$ 中点时， $A M$ 的大小为．

查看试题解析

三、解答题

15. 计算： $\sqrt{8} - 4 \cos 45 ° + {(- 1)}^{2000} + | \sqrt{2} - 1 |$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中点D，E，F分别在 $A B$ ， $B C$ ， $A C$ 边上， $D E // A C$ ， $E F // A B$ .

(1)、求证： $△ B D E \sim △ E F C$ ；

(2)、若 $\frac{A F}{F C} = \frac{1}{2}$ ， $△ E F C$ 的面积是20，求 $△ A B C$ 的面积.

查看试题解析
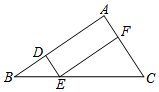17. 如图所示的平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (- 3 ， 2) ， B (- 1 ， 3) ， C (- 1 ， 1)$ ，请按如下要求画图：

⑴以坐标原点O为旋转中心，将 $△ A B C$ 顺时针旋转90°，得到 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ ；

⑵以坐标原点O为位似中心，在x轴下方，画出 $△ A B C$ 的位似图形 $△ A_{2} B_{2} C_{2}$ ，使它与 $△ A B C$ 的位似比为 $2： 1$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中 $∠ C = 90 °$ ， $∠ B = 30 °$ ， $A D$ 是 $∠ B A C$ 的平分线，与 $B C$ 相交于点D ，且 $A B = 4 \sqrt{3}$ ，求 $A D$ 的长．

查看试题解析
19. 如图，反比例函数 $y = \frac{k}{x}$ 的图象与一次函数 $y = a x + b$ 的图象交于点A，B，点B的纵坐标是 $- 1$ ，过点A作 $A C ⊥ x$ 轴于点C，且 $O C = 1$ ， $△ A O C$ 的面积为1．

(1)、求反比例函数和一次函数表达式；

(2)、若点D是反比例函数图象上一点，且到点A，C的距离相等，求点D的坐标．

查看试题解析
20. 图1是某种路灯的实物图片，图2是该路灯的平面示意图， $M N$ 为立柱的一部分，灯臂 $A C$ ，支架 $B C$ 与立柱 $M N$ 分别交于A，B两点，灯臂 $A C$ 与支架 $B C$ 交于点C，已知 $∠ M A C = 60 °$ ， $∠ A C B = 15 °$ ， $A C = 40 cm$ ，求支架 $B C$ 的长.（结果精确到 $1cm$ ，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ， $\sqrt{6} \approx 2.449$ ）

查看试题解析
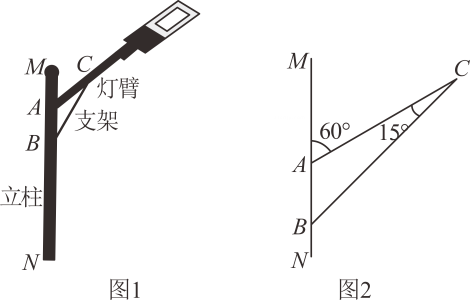21. 如图，点A，B，C是半径为2的⊙O上三个点，AB为直径，∠BAC的平分线交圆于点D，过点D作AC的垂线交AC得延长线于点E，延长线ED交AB得延长线于点F．

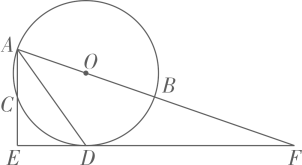(1)、判断直线EF与⊙O的位置关系，并证明．

(2)、若DF= $4 \sqrt{2}$ ，求tan∠EAD的值．

查看试题解析
22. 如图，已知抛物线 $y = - x^{2} + b x + c$ 与x轴交于点 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与y轴交于点C ，点P是抛物线上在第一象限内的一动点，且点P的横坐标为t ．

(1)、求抛物线的表达式；

(2)、连接 $B C$ ， $P B$ ， $P C$ ，设 $△ P B C$ 的面积为S ，求S与t的函数表达式，并求S最大时点P的坐标．

查看试题解析
23. 如图，正方形 $A B C D$ 的边长为2，点P为 $B C$ 边上一点，以 $A P$ 为斜边在正方形 $A B C D$ 内部作等腰直角三角形 $A P Q$ ，连接 $A C$ 交 $P Q$ 于点E，连接 $D Q$ ．

(1)、求证： $△ A C P ∽ △ A D Q$ ；

(2)、当点P为 $B C$ 的中点时，
①求 $\frac{P E}{P C}$ 的值；

②求证： $E Q = \frac{\sqrt{5}}{2} D Q$ ．

查看试题解析