安徽省亳州市蒙城县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 关于二次函数 $y = - x^{2} - 2$ 下列说法正确的是（）．

A、有最大值-2 B、有最小值-2 C、对称轴是 $x = 1$ D、对称轴是 $x = - 1$

查看试题解析
2. 对抛物线y=-x²+4x-3而言，下列结论正确的是（）

A、开口向上 B、与y轴的交点坐标是(0，3) C、与两坐标轴有两个交点 D、顶点坐标是（2，1）

查看试题解析
3. 点P₁（﹣1， $y_{1}$ ），P₂（3， $y_{2}$ ），P₃（5， $y_{3}$ ）均在二次函数 $y = - x^{2} + 2 x + c$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{3} > y_{2} > y_{1}$ B、 $y_{3} > y_{1} = y_{2}$ C、 $y_{1} > y_{2} > y_{3}$ D、 $y_{1} = y_{2} > y_{3}$

查看试题解析
4. 如图，在△ABC中，AB=3，BC=5.2，∠B=60°，将△ABC绕点A逆时针旋转△ADE，若点B的对应点D恰好落在BC边上时，则CD的长为（）

A、0.8 B、2 C、2.2 D、2.8

查看试题解析
5. 如图，在直角坐标系中，△OAB的顶点为O(0，0)，A(-6，4)，B(-3，0)．以点O为位似中心，在第四象限内作与△OAB的位似比为 $\frac{1}{2}$ 的位似图形△OCD，则点C坐标为（ )

A、(2，-1) B、(3，-2) C、 $(\frac{3}{2} ， - \frac{3}{2})$ D、 $(\frac{3}{2} ， - 1)$

查看试题解析
6. 如图，已知点A为反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象上一点，过点A作 $A B ⊥ y$ 轴，垂足为B，若 $Δ O A B$ 的面积为3，则k的值为（）

A、3 B、-3 C、6 D、-6

查看试题解析
7. 若ad=bc，则下列不成立的是（）

A、 $\frac{a}{b} = \frac{c}{d}$ B、 $\frac{a - c}{b - d} = \frac{a}{b}$ C、 $\frac{a + b}{b} = \frac{c + d}{d}$ D、 $\frac{a + 1}{b + 1} = \frac{c + 1}{d + 1}$

查看试题解析
8. 如图，四边形 $O A B C$ 是矩形，四边形 $A D E F$ 是边长为3的正方形，点 $A$ ， $D$ 在 $x$ 轴的正半轴上，点 $C$ 在 $y$ 轴的正半轴上，点 $F$ 在边 $A B$ 上，点 $B$ 、 $E$ 在双曲线 $y = \frac{k}{x} (x > 0)$ 上，且 $B F = 5$ ，则 $k$ 值为（）．

A、15 B、 $\frac{71}{4}$ C、 $\frac{72}{5}$ D、17

查看试题解析
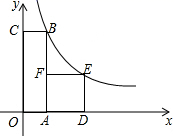9. 如图，抛物线y=ax²+bx+c经过(-1，0)和(0，-1)两点，则抛物线y=cx²+bx+a的图像大致为（ )

A、 B、 C、 D、

查看试题解析
10. 正方形ABCD中，AB=4，P为对角线BD上一动点，F为射线AD上一点，若AP=PF，则△APF的面积最大值为（）

A、8 B、6 C、4 D、 $2 \sqrt{2}$

查看试题解析

二、填空题

11. 抛物线 $y = - {(x + 2)}^{2}$ 的顶点坐标是．

查看试题解析
12. 如图，若芭蕾舞者拍起的脚尖点C分线段AB近似于黄金分割(AC $<$ BC)，已知AB=160cm，BC的长约为cm．(结果精确到0.1cm)

查看试题解析
13. 如图，在边长为1的小正方形网格中，点A、B、C均在格点上，则tan∠B的值为．

查看试题解析
14. 如图，矩形ABCD中，AB=6，AD=8，点P是AB边上一动点，把△ADP沿DP折叠得△ $A^{'} D P$ ，射线 $D A^{'}$ 交直线AB于点Q点．

(1)、当Q点和B点重合时，PQ长为；

(2)、当△ $A^{'} D C$ 为等腰三角形时，DQ长为．

查看试题解析

三、解答题

15. 计算：2sin²45°-6cos30°+ 3tan45°+4sin60°

查看试题解析
16. 如图，二次函数y=- $\frac{1}{2} x^{2}$ +bx+c的图象经过A(2，0)、B(0，-4)两点，

(1)、求二次函数的解析式；

(2)、设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．

查看试题解析
17. 如图，一次函数y₁=kx+b的图象与反比性函数y₂= $\frac{m}{x}$ 的图象交于A(2，1)、B（-1，n）两点．

(1)、利用图中的条件，求反比例函数和一次函数的解析式；

(2)、根据图象直接写出使y₁ $<$ y₂的自变量x取值范围．

查看试题解析
18. 如图，在网格图中（小正方形的边长为1）， $△ A B C$ 的三个顶点都在格点上．

(1)、①把 $△ A B C$ 沿着 $x$ 轴向右平移6个单位得到 $△ A_{1} B_{1} C_{1}$ ，请你画出 $△ A_{1} B_{1} C_{1}$ ；
②请你以坐标系的原点 $O$ 点为位似中心在第一象限内画出 $△ A B C$ 的位似图形 $△ A_{2} B_{2} C_{2}$ ，使得 $△ A B C$ 与 $△ A_{2} B_{2} C_{2}$ 的位似比为1：2；

(2)、请你直接写出 $△ A_{2} B_{2} C_{2}$ 三个顶点的坐标．

查看试题解析
19. 2020年6月23日，我国第55颗北斗卫星，即北斗全球卫星导航系统最后一颗组网卫星发射成功北斗导航装备的不断更新，极大方便人们的出行，某中学从A地出发．组织学生利用导航到C地区进行研学活动，出发时发现C地恰好在A地正北方向，且距离A地24千米，由于A、C两地间是一块湿地．所以导航显示的路线是沿北偏东60°方向走到B地，再沿北编西37°方向走一段距离才能到达C地，求A、B两地的距离(精确到1千米)．(参考数据sin37°=0.6，cos37°=0.8，tan37°=0.7， $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7)

查看试题解析
20. 已知：如图，在 $Rt △ A B C$ 中， $∠ B A C = 90 °$ ， $A D ⊥ B C$ 于 $D$ ， $E$ 为直角边 $A C$ 的中点，射线 $E D$ 交 $A B$ 的延长线于点 $F$ ．

(1)、若 $A B = 6$ ， $A C = 8$ ，求 $B D$ 长；

(2)、求证： $A B \cdot A F = A C \cdot DF$ ．

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $∠ A B C = 90^{°} ， ∠ C = 45^{°} ， C D = \sqrt{2} ， B D = 3$ .

(1)、求 $\sin ∠ C B D$ 的值；

(2)、若 $A B = 3$ ，求 $A D$ 的长．

查看试题解析
22. 如图，已知抛物线 $y_{1} = a (x - 1) (x - 5)$ 和直线 $y_{2} = - a x - a$ （其中 $a > 0$ ）相交于 $A$ ， $B$ 两点，抛物线 $y_{1}$ 与 $x$ 轴交于 $C$ ， $D$ 两点，与 $y$ 轴交于点 $G$ ，直线 $y_{2}$ 与坐标轴交点于 $E$ ， $F$ 两点．

(1)、若 $G$ 的坐标为 $(0 ， 5)$ ，求抛物线 $y_{1}$ 的解析式和直线 $y_{2}$ 的解析式；

(2)、求证：直线 $y_{2} = - a x - a$ 始终经过该抛物线 $y_{1}$ 的顶点；

(3)、求 $\frac{A B + E F}{A F}$ 的值．

查看试题解析
23. 如图1， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $E$ 为 $△ A B C$ 的中线 $B D$ 上的一点，将线段 $A E$ 以 $E$ 点为中心逆时针旋转90度得到线段 $E F$ ， $E F$ 恰好经过点 $C$ ．

(1)、若 $∠ C A F = α$ ，则 $∠ C B E =$ ；（用含 $α$ 的代数式表示）

(2)、过点 $C$ 作 $C H // A E$ ，交 $A F$ 于点 $H$ ，连接 $B H$ ，交 $E F$ 于点 $G$ ．
①求证： $A F = B H$ ；

②若 $C F = 2$ ，求 $E G$ 的长．

查看试题解析