安徽省安庆市宿松县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 抛物线 的顶点坐标是( )A、 B、 C、 D、2. 若反比例函数 ,当 时,y随x的增大而增大,则k的取值范围是( )A、 B、 C、 D、3. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
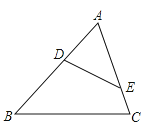 A、∠AED=∠B B、∠ADE=∠C C、= D、=4. 二次函数 ,当 时,函数值y的取值范围是( )A、 B、 C、 D、5. 比萨斜塔是意大利的著名建筑,其示意图如图所示.设塔顶中心点为点B,塔身中心线 与垂直中心线 的夹角为 ,过点B向垂直中心线 引垂线,垂足为点D.通过测量可得 、 、 的长度,利用测量所得的数据计算 的三角函数值,进而可求 的大小.下列关系式正确的是( )
A、∠AED=∠B B、∠ADE=∠C C、= D、=4. 二次函数 ,当 时,函数值y的取值范围是( )A、 B、 C、 D、5. 比萨斜塔是意大利的著名建筑,其示意图如图所示.设塔顶中心点为点B,塔身中心线 与垂直中心线 的夹角为 ,过点B向垂直中心线 引垂线,垂足为点D.通过测量可得 、 、 的长度,利用测量所得的数据计算 的三角函数值,进而可求 的大小.下列关系式正确的是( )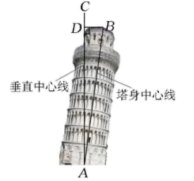 A、 B、 C、 D、6. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力等因素,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
A、 B、 C、 D、6. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力等因素,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度大于 ;②足球飞行路线的对称轴是直线 ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是 ,其中正确结论的个数是( )
A、1 B、2 C、3 D、47. 如图, 中, ,点D在 上, .若 , ,则 的长度为( ) A、 B、 C、 D、48. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线 与直线 的“和谐值”为( )A、3 B、 C、 D、29. 如图,在 中, ,以其三边为边向外作正方形,过点C作 于点R,再过点C作 分别交边 , 于点P,Q.若 , ,则 的长为( )
A、 B、 C、 D、48. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线 与直线 的“和谐值”为( )A、3 B、 C、 D、29. 如图,在 中, ,以其三边为边向外作正方形,过点C作 于点R,再过点C作 分别交边 , 于点P,Q.若 , ,则 的长为( )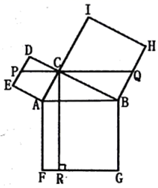 A、14 B、9 C、 D、10. 如图,矩形 中, , ,动点P从A点出发,按 的方向在 和 上移动,记 ,点D到直线 的距离为y,则y关于x的函数图象大致是( )
A、14 B、9 C、 D、10. 如图,矩形 中, , ,动点P从A点出发,按 的方向在 和 上移动,记 ,点D到直线 的距离为y,则y关于x的函数图象大致是( ) A、
A、 B、
B、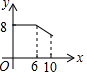 C、
C、 D、
D、
二、填空题
-
11. 如图,扇子的圆心角为 ,余下扇形的圆心角为 ,x与y的比通常按黄金比来设计,这样的扇子外形比较美观,若黄金比取0.6,则y的值为 .
 12. 如图,小明在A时测得某树的影长为 ,B时又测得该树的影长为 ,若两次日照的光线互相垂直,则树的高度为m.
12. 如图,小明在A时测得某树的影长为 ,B时又测得该树的影长为 ,若两次日照的光线互相垂直,则树的高度为m. 13. 如图,一次函数 的图象与x轴和y轴分别交于点A和点B.与反比例函数 的图象在第一象限内交于点C, 轴, 轴.垂足分别为点D,E.当矩形 的面积是 的面积2倍时,k的值为 .
13. 如图,一次函数 的图象与x轴和y轴分别交于点A和点B.与反比例函数 的图象在第一象限内交于点C, 轴, 轴.垂足分别为点D,E.当矩形 的面积是 的面积2倍时,k的值为 . 14. 在 中, , ,将 绕顶点O顺时针旋转,旋转角为 ,得到 .
14. 在 中, , ,将 绕顶点O顺时针旋转,旋转角为 ,得到 .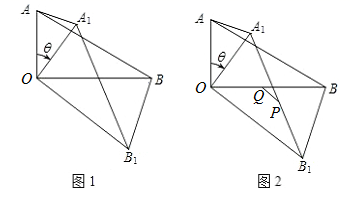 (1)、如图1,连接 、 ,设 和 的面积分别为 、 .则 .(2)、如图2,设 中点为Q, 中点为P,连接 ,若 ,当 时,线段 长度最小,最小值为 .
(1)、如图1,连接 、 ,设 和 的面积分别为 、 .则 .(2)、如图2,设 中点为Q, 中点为P,连接 ,若 ,当 时,线段 长度最小,最小值为 .三、解答题
-
15. 计算: .16. 已知二次函数的图象经过原点及点 ,且图象与x轴的另一交点到原点的距离为1,求该二次函数的解析式.17. 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1
和△A2B2C2:

⑴将△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
⑵以图中的点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 .
18. 如图,已知四边形 是矩形,点E在 的延长线上, .连 与 相交于点F, ,若 ,求 的值. 19. 为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表:
19. 为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表:名称
红外线体温检测仪
安装示意图

技术参数
探测最大角:
探测最小角:
安装要求
本设备需安装在垂直于水平地面 的支架 上
根据以上内容,解决问题:
学校要求测温区域的宽度 为 ,请你帮助学校确定该设备的安装高度 .(参考数据 , , , , )
20. 直线 与反比例函数 的图象分别交于点 和点 ,与坐标轴分别交于点C和点D. (1)、求直线 的解析式;(2)、观察图象,当 时,直接写出 的解集;(3)、若点P是y轴上一动点,当 与 相似时,直接写出点P的坐标.21. 如图,O为线段 的中点, 与 交于点H, ,且 交 于D, 交 于E.
(1)、求直线 的解析式;(2)、观察图象,当 时,直接写出 的解集;(3)、若点P是y轴上一动点,当 与 相似时,直接写出点P的坐标.21. 如图,O为线段 的中点, 与 交于点H, ,且 交 于D, 交 于E. (1)、写出图中两对相似三角形;并证明其中一对.(2)、连接 ,如果 , , ,求 的长.22. 小红经营的网店以销售文具为主,其中一款笔记本进价为10元/本,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:本)与线下售价x(单位:元/本, ,且x为整数)满足一次函数的关系,部分数据如下表:
(1)、写出图中两对相似三角形;并证明其中一对.(2)、连接 ,如果 , , ,求 的长.22. 小红经营的网店以销售文具为主,其中一款笔记本进价为10元/本,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:本)与线下售价x(单位:元/本, ,且x为整数)满足一次函数的关系,部分数据如下表:x(元/本)
12
13
14
15
16
y(本)
120
110
100
90
80
(1)、求y与x的函数关系式;(2)、若线上售价始终比线下每本便宜1元,且线上的月销量固定为40件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.23. 锐角 中, , ,两动点M,N分别在边 , 上滑动,且 ,以 为边向下作正方形 ,设其边长为x,正方形 与 公共部分的面积为 (1)、 中边 上高 ;(2)、当 恰好落在边 上时,求x的值(如图1);(3)、当 在 外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
(1)、 中边 上高 ;(2)、当 恰好落在边 上时,求x的值(如图1);(3)、当 在 外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?