安徽省安庆市望江县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 已知 ,则 的值为( )A、 B、1 C、2 D、不能确定2. 在 中, , ,则 的值为( )A、 B、 C、 D、23. 如图, , ,若 ,则CE的长是( )
 A、 B、2 C、 D、54. 在二次函数 中,函数y与自变量x的部分对应值如下表:
A、 B、2 C、 D、54. 在二次函数 中,函数y与自变量x的部分对应值如下表:x
……
-1
1
3
4
……
y
……
-6
m
n
……
则m、n的大小关系为( )
A、 B、 C、 D、无法确定5. 已知反比例函数 的图象如图所示,则二次函数 的图象大致为( ). A、
A、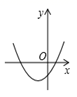 B、
B、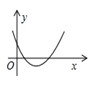 C、
C、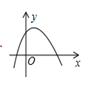 D、
D、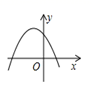 6. 如图,在正方形网格上有两个相似三角形 和 ,则 的度数为( )
6. 如图,在正方形网格上有两个相似三角形 和 ,则 的度数为( ) A、135° B、90° C、60° D、45°7. 如图所示, 是 的外接圆,已知 ,则 的大小为( )
A、135° B、90° C、60° D、45°7. 如图所示, 是 的外接圆,已知 ,则 的大小为( ) A、50° B、55° C、65° D、75°8. 已知直线 ( ,k是常数)与双曲线 交于点 , 两点,则 的值为( )A、5 B、0 C、-5 D、-109. 点 均在抛物线 上,下列说法正确的是( )
A、50° B、55° C、65° D、75°8. 已知直线 ( ,k是常数)与双曲线 交于点 , 两点,则 的值为( )A、5 B、0 C、-5 D、-109. 点 均在抛物线 上,下列说法正确的是( ) A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则10. 如图,点A是反比例函数 的图象上任意-点, 轴交反比例函数 的图象于点B , 以AB为边作平行四边形ABCD , 其中C , D在x轴上,则平行四边形ABCD的面积为( )
A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则10. 如图,点A是反比例函数 的图象上任意-点, 轴交反比例函数 的图象于点B , 以AB为边作平行四边形ABCD , 其中C , D在x轴上,则平行四边形ABCD的面积为( ) A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
11. 中, , , ,则 的外接圆半径长是 .12. 我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L , 圆的直径为d , 如图所示,当n=6时,π≈ = =3,那么当n=12时,π≈ ≈(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
 13. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A , B , E在x轴上,若正方形BEFG的边长为5,则C点坐标为 .
13. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A , B , E在x轴上,若正方形BEFG的边长为5,则C点坐标为 . 14. 二次函数 ( ,a , b , c是常数)图象如图,下列结论:
14. 二次函数 ( ,a , b , c是常数)图象如图,下列结论:① ;② ;③当 时, ;④ .
其中正确的有 . (填上你认为正确的结论前的序号).
 15. 如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
15. 如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
⑴作出与△ABC关于x轴对称的△A 1B1C1 , 并写出点A1的坐标;
⑵以原点O 为位似中心,在原点的另一侧画出△A2B2C2 , 使 = ,并写出点A2的坐标.
三、解答题
-
16. 计算: .17. 图1是室内篮球机,图2是篮球机的侧面图.已知 , , , ,在E处测得点D的仰角为50°,在A处测得篮筐C的仰角为40°, , , ,求篮筐C距地面 的高度(参考数据: , , )
 18. 如图在锐角三角形OAB中,点M , N分别在边OB , OA上, 于点G , 于点H , .
18. 如图在锐角三角形OAB中,点M , N分别在边OB , OA上, 于点G , 于点H , . (1)、求证: ;(2)、若 , ,求 的值.19. 一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数 ,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠半分钟末的速度为0.5米/分.
(1)、求证: ;(2)、若 , ,求 的值.19. 一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数 ,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠半分钟末的速度为0.5米/分.
求:
(1)、弹珠离开轨道时的速度.(2)、二次函数和反比例函数的关系式;20. 如图:已知AB为圆O的直径,CD是弦,且 于点E , 连结AC , OC , BC . (1)、求证: ;(2)、若 , ,求圆O的直径;(3)、在(2)的前提下,求劣弧BC的长.21. 世纪华联超市准备进一批每个进价为35元的小家电,经市场调查预测,当每个售价定为45元时可售出360个:每个定价每增加1元,销售量将减少6个.(1)、设每个定价增加x元,此时的销售量是多少?(用含x的代数式表示)(2)、世纪华联超市若准备获得利润7200元,并且使进货量较少,则每个应定价为多少元?(3)、世纪华联超市若要获得最大利润,则每个应定价多少元?22. 如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E , 过点E作EF⊥AB交边AC于点F , 射线ED交射线AC于点G .
(1)、求证: ;(2)、若 , ,求圆O的直径;(3)、在(2)的前提下,求劣弧BC的长.21. 世纪华联超市准备进一批每个进价为35元的小家电,经市场调查预测,当每个售价定为45元时可售出360个:每个定价每增加1元,销售量将减少6个.(1)、设每个定价增加x元,此时的销售量是多少?(用含x的代数式表示)(2)、世纪华联超市若准备获得利润7200元,并且使进货量较少,则每个应定价为多少元?(3)、世纪华联超市若要获得最大利润,则每个应定价多少元?22. 如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E , 过点E作EF⊥AB交边AC于点F , 射线ED交射线AC于点G . (1)、求证:△EFG∽△AEG;(2)、设FG=x , △EFG的面积为y , 求y关于x的函数解析式并写出定义域;(3)、联结DF , 当△EFD是等腰三角形时,请直接写出FG的长度.
(1)、求证:△EFG∽△AEG;(2)、设FG=x , △EFG的面积为y , 求y关于x的函数解析式并写出定义域;(3)、联结DF , 当△EFD是等腰三角形时,请直接写出FG的长度.