安徽省安庆市太湖县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 下列函数中,是二次函数的有( )
① ② ③ ④
A、1个 B、2个 C、3个 D、4个2. 若要得到函数 的图象,只需将函数 的图象( )A、先向右平移1个单位长度,再向上平移2个单位长度 B、先向左平移1个单位长度,再向上平移2个单位长度 C、先向左平移1个单位长度,再向下平移2个单位长度 D、先向右平移1个单位长度,再向下平移2个单位长度3.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )
 A、7海里 B、14海里 C、3.5海里 D、4海里4. 若 为实数,关于 的方程 的两个非负实数根为 、 ,则代数式 的最小值是( ).A、-15 B、-16 C、15 D、165. 如图,P是双曲线上一点,且图中的阴影部分的面积为3,则此反比例函数的解析式为( )
A、7海里 B、14海里 C、3.5海里 D、4海里4. 若 为实数,关于 的方程 的两个非负实数根为 、 ,则代数式 的最小值是( ).A、-15 B、-16 C、15 D、165. 如图,P是双曲线上一点,且图中的阴影部分的面积为3,则此反比例函数的解析式为( ) A、 B、 C、 D、6. 如图,已知DE∥BC,EF∥AB,现得到下列结论:
A、 B、 C、 D、6. 如图,已知DE∥BC,EF∥AB,现得到下列结论:① ;② ;③ ;④ .
其中正确比例式的个数有( )
 A、4个 B、3个 C、2个 D、1个7. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△CDF:S四边形ABFE等于( )
A、4个 B、3个 C、2个 D、1个7. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△CDF:S四边形ABFE等于( )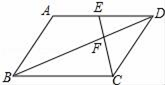 A、1:3 B、2:5 C、3:5 D、4:98. 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
A、1:3 B、2:5 C、3:5 D、4:98. 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )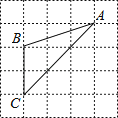 A、 B、 C、 D、9. 二次函数 的图象如图所示,下列结论:① ;② ;③m为任意实数,则 ;④ ;⑤若 且 ,则 .其中正确的有( )
A、 B、 C、 D、9. 二次函数 的图象如图所示,下列结论:① ;② ;③m为任意实数,则 ;④ ;⑤若 且 ,则 .其中正确的有( ) A、①④ B、③④ C、②⑤ D、②③⑤10. 如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )
A、①④ B、③④ C、②⑤ D、②③⑤10. 如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )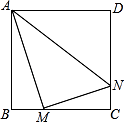 A、8 B、4 C、10 D、8
A、8 B、4 C、10 D、8二、填空题
-
11. 已知二次函数 的图象如图所示,则关于x的一元二次方程 的根为 .
 12. 如图,已知线段AB=a,C,C′是线段AB的两个黄金分割点,则CC′= .
12. 如图,已知线段AB=a,C,C′是线段AB的两个黄金分割点,则CC′= . 13. 已知a、b、c是 的三边长,且a、b、c满足 ,若 ,则 的值为 .14. 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E . 若B′恰好落在射线CD上,则BE的长为 .
13. 已知a、b、c是 的三边长,且a、b、c满足 ,若 ,则 的值为 .14. 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E . 若B′恰好落在射线CD上,则BE的长为 .
三、解答题
-
15. 计算:16. 下表给出了代数式 与x的一些对应值:
x
…
-2
-1
0
1
2
3
…
…
5
n
c
2
-3
-10
…
(1)、根据表格中的数据,确定b,c,n的值;(2)、设 ,直接写出 时,y的最大值.17. 已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.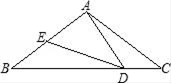 (1)、求证:△BDE∽△CAD;(2)、若CD=2,求BE的长.18. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)、求证:△BDE∽△CAD;(2)、若CD=2,求BE的长.18. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
⑴画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是 ▲ ;
⑵以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ▲ .
19. 如图,直线y1=﹣x+4,y2= x+b都与双曲线y= 交于点A(1,m),这两条直线分别与x轴交于B,C两点.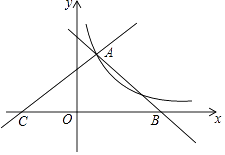 (1)、求y与x之间的函数关系式;
(1)、求y与x之间的函数关系式;
(2)、直接写出当x>0时,不等式 x+b> 的解集;(3)、若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.20. 如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好.此时,路灯的灯柱AB的高应该设计为多少米.(结果保留根号)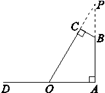 21. 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(点P不与A、D重合),PE⊥BP,PE交DC于点E.
21. 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(点P不与A、D重合),PE⊥BP,PE交DC于点E. (1)、求证:△ABP∽△DPE;(2)、设AP=x,DE=y,求y与x之间的函数关系式,并写出x的取值范围;(3)、请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由.22. “扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量 (件)与销售单价 (元)之间存在一次函数关系,如图所示.
(1)、求证:△ABP∽△DPE;(2)、设AP=x,DE=y,求y与x之间的函数关系式,并写出x的取值范围;(3)、请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由.22. “扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量 (件)与销售单价 (元)之间存在一次函数关系,如图所示. (1)、求 与 之间的函数关系式;(2)、如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.23. 如图
(1)、求 与 之间的函数关系式;(2)、如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.23. 如图 (1)、(感知)
(1)、(感知)
如图①,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,∠AEB=90°,求证: = .(2)、(探究)
如图②,在四边形ABCD中,∠C=∠ADC=90°,点E在边CD上,点F在边AD的延长线上,∠FEG=∠AEB=90°,且 = ,连接BG交CD于点H.求证:BH=GH.(3)、(拓展)
如图③,点E在四边形ABCD内,∠AEB+∠DEC=180°,且 = ,过E作EF交AD于点F,若∠EFA=∠AEB,延长FE交BC于点G.求证:BG=CG.