安徽省芜湖市无为市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列条件中，不能判定△ABC是等腰三角形的是（）

A、a=3，b=3，c=4 B、a︰b︰c=2︰3︰4 C、∠B=50°，∠C=80° D、∠A︰∠B︰∠C=1︰1︰2

查看试题解析
3. 叶绿体是植物进行光合作用的场所，叶绿体DNA最早发现于衣藻叶绿体，长约0.00005米．其中，0.00005用科学记数法表示为（　　）

A、0.5×10^﹣⁴ B、5×10^﹣⁴ C、5×10^﹣⁵ D、50×10^﹣³

查看试题解析
4. 一个正多边形每个外角都是30°，则这个多边形边数为（）

A、10 B、11 C、12 D、13

查看试题解析
5. 如图，Rt△ABC中，∠ACB＝90°，∠A＝55°，将其折叠，使点A落在边CB上 $A^{'}$ 处，折痕为CD，则 $∠ A^{'} D B$ ＝（）

A、40° B、30° C、20° D、10°

查看试题解析
6. 如图，AC与BD相交于点O，∠D=∠C，添加下列哪个条件后，仍不能使△ADO≌△BCO的是（）

A、AD=BC B、AC=BD C、OD=OC D、∠ABD=∠BAC

查看试题解析
7. 若关于x的方程 $\frac{m}{x - 4} - \frac{1 - x}{4 - x} = 0$ 无解，则m的值是（）

A、 $- 2$ B、2 C、 $- 3$ D、3

查看试题解析
8. 已知 $x + \frac{1}{x} = 3$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值为（）

A、6 B、7 C、9 D、11

查看试题解析
9. 若 $a + b = 3$ ，则 $a^{2} - b^{2} + 6 b$ 的值为（）

A、3 B、6 C、9 D、12

查看试题解析
10. 某小区有一块边长为a的正方形场地，规划修建两条宽为b的绿化带. 方案一如图甲所示，绿化带面积为S_甲：方案二如图乙所示，绿化带面积为S_乙. 设 $k = \frac{S_{甲}}{S_{乙}} (a > b > 0)$ ，下列选项中正确的是（）

A、 $0 < k < \frac{1}{2}$ B、 $\frac{3}{2} < k < 2$ C、 $1 < k < \frac{3}{2}$ D、 $\frac{1}{2} < k < 1$

查看试题解析

二、填空题

11. 若 $3^{2} \times 9^{2 n + 1} \div 27^{n + 1} = 81$ ，则 $n =$ ．

查看试题解析
12. 若 $x^{2} + k x + \frac{9}{4}$ 是一个完全平方式，则k的值为．

查看试题解析
13. 如图所示， $△ B D C'$ 是将长方形纸牌ABCD沿着BD折叠得到的，图中 $($ 包括实线、虚线在内 $)$ 共有全等三角形对

查看试题解析
14. 如图，在 $Rt △ A B C$ 中． $A C ⊥ B C$ ，若 $A C = 5$ ， $B C = 12$ ， $A B = 13$ ，将 $Rt △ A B C$ 折叠，使得点C恰好落在AB边上的点E处，折痕为AD，点P为AD上一动点，则 $△ P E B$ 的周长最小值为．

查看试题解析

三、解答题

15. 观察下列各式：
$(x - 1) (x + 1) = x^{2} - 1$ ；

$(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ；

$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；

……

(1)、 $(x - 1) (x^{4} + x^{3} + x^{2} + x + 1) =$ ；

(2)、根据规律可得： $(x - 1) (x^{n - 1} + \dots + x + 1) =$ （其中n为正整数）；

(3)、计算： $(3 - 1) (3^{50} + 3^{49} + 3^{48} + \dots + 3^{2} + 3 + 1)$ ；

查看试题解析
16. 因式分解：

(1)、 $2 a^{4} - 32$

(2)、 $(a - 4 b) (a + b) + 3 a b$

查看试题解析
17. 解方程： $\frac{x}{x - 2} - 1 = \frac{3}{x (x - 2)}$ ．

查看试题解析
18. 已知a+b=2，求（ $\frac{1}{a} + \frac{1}{b}$ ）· $\frac{a b}{{(a - b)}^{2} + 4 a b}$ 的值．

查看试题解析
19.
作图题：（不要求写作法）如图，△ABC在平面直角坐标系中，其中，点A，B，C的坐标分别为A（﹣2，1），B（﹣4，5），C（﹣5，2）．

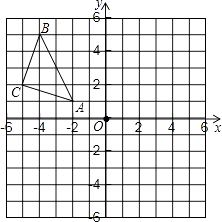(1)、作△ABC关于y轴对称的△A₁B₁C₁ ，其中，点A、B、C的对应点分别为A₁、B₁、C₁；

(2)、写出点A₁、B₁、C₁的坐标．

查看试题解析
20. 如图，△ABC和△DBE均为等腰直角三角形，且点B为直角顶点．求证：AD＝EC．

查看试题解析
21. 列方程解应用题：
中华优秀传统文化是中华民族的“根”和“魂”，是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化，某校为各班购进《三国演义》和《水浒传》连环画若干套，其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元，用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍，求每套《水浒传》连环画的价格．

查看试题解析
22. 如图1，将一个长为4a，宽为2b的长方形，沿图中虚线均分成4个长方形，然后按图2形状拼成一个正方形．

(1)、图2中阴影部分的边长是（用含a、b的式子表示）；

(2)、若2a+b＝7，且ab＝3，求图2中阴影部分的面积；

(3)、观察图2，用等式表示出（2a﹣b）² ， ab，（2a+b）²的数量关系是．

查看试题解析
23.

(1)、如图1， $A (0 ， a)$ ， $B (b ， 0)$ ．若a，b满足 $2 a^{2} + b^{2} + 2 a b - 4 a + 4 = 0$ ，求A、B的坐标．

(2)、在（1）的条件下，点C为线段AB上的一点， $A E ⊥ O C$ ， $B F ⊥ O C$ ，垂足分别为E、F、若 $A E = m$ ， $B F = n$ ， $m - n = 1$ ，求线段EF的长．

(3)、如图2， $A (0 ， a)$ ， $B (b ， 0)$ ，点P为 $△ A B O$ 的角平分线的交点，若a，b满足 $a + b = 0$ ， $P N ⊥ P A$ 交x轴于N，延长OP交AB于M，直接写出AB、ON、PM之间的数量关系（不需要写出证明过程）．

查看试题解析