安徽省铜陵市铜官区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 现有两根木棒，它们的长分别是30cm和80cm，若要钉成一个三角形木架，则应选取的第三根木棒长为（）

A、40cm B、50cm C、60cm D、130cm

查看试题解析
2. 低碳环保理念深入人心，共享单车已成为出行新方式．下列共享单车图标，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各分式正确的是（）

A、 $\frac{b}{a} = \frac{b^{2}}{a^{2}}$ B、 $\frac{a^{2} + b^{2}}{a + b} = a + b$ C、 $\frac{a^{2} - 2 a + 1}{1 - a} = 1 - a$ D、 $\frac{3 x - 4 y}{8 x y - 6 x^{2}} = \frac{1}{2 x}$

查看试题解析
4. 如图，已知 $△ A B E ≅ △ A C D$ ， $∠ 1 = ∠ 2$ ， $∠ B = ∠ C$ ，则下列结论错误的是（）

A、 $A B = A C$ B、 $∠ B A E = ∠ C A D$ C、 $B E = C D$ D、 $A D = D E$

查看试题解析
5. 如图，△ACB ≌△A′CB′，∠A′CB=30°，∠ACB′=110°，则∠ACA′的度数是（）

A、 $20 °$ B、 $30 °$ C、 $35 °$ D、 $40 °$

查看试题解析
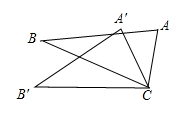6. 若x²﹣mx+16是完全平方式，则m的值等于（）

A、2 B、4或﹣4 C、2或﹣2 D、8或﹣8

查看试题解析
7. 能使分式 $\frac{x^{2} - x}{x^{2} - 1}$ 的值为零的所有x的值是（）

A、x=0 B、x=1 C、x=0或x=1 D、x=0或x=±1

查看试题解析
8. 一个多边形截取一个角后，形成另一个多边形的内角和是1620°，则原来多边形的边数是（）

A、10 B、11 C、12 D、以上都有可能

查看试题解析
9. 已知分式方程 $\frac{2 x + m}{x - 1} = 1$ 的解是非负数，则 $m$ 的取值范围是（）

A、 $m \leq - 1$ B、 $m \leq - 1$ 且 $m \neq - 2$ C、 $m \geq - 1$ D、 $m \geq - 1$ 且 $m \neq 2$

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ C = 90^{\circ} ， A D$ 平分 $∠ B A C ， D E ⊥ A B$ 于点 $E ，$ 给出下列结论． $① C D = E D$ ； $② A C + B E = A B ，$ ③ $∠ B D E = ∠ B A C$ ， $④ D A$ 平分 $∠ C D E$ ， $⑤ S_{△ B D E} ： S_{△ A C D} = A B ： A C$ 其中正确的有（）个

A、 $5$ B、 $4$ C、 $3$ D、 $2$

查看试题解析

二、填空题

11. 点P（1，n）和点Q（n﹣1，2m）关于x轴对称，则m+n的值为．

查看试题解析
12. 已知等腰三角形一腰上的高与另一腰的夹角为50°，则等腰三角形的顶角度数为．

查看试题解析
13. 如图，已知△ABC，BC=10，BC边的垂直平分线交AB，BC于点E、D．若△ACE的周长为12，则△ABC的周长为．

查看试题解析
14. 已知：2x+3y+3＝0，计算：4^x•8^y的值＝．

查看试题解析
15. △ABC中，∠ABC和∠ACB的平分线交于点O，OD⊥BC于D， $△$ ABC的面积18，AB=6，AC=8，OD=2，则BC的长是．

查看试题解析
16. 如图，OA，OB分别是线段MC、MD的垂直平分线，MD＝5cm，MC＝7cm，CD＝10cm，一只小蚂蚁从点M出发，爬到OA边上任意一点E，再爬到OB边上任意一点F，然后爬回M点，则小蚂蚁爬行的最短路径的长度为．

查看试题解析

三、解答题

17. 解方程： $\frac{3}{2} - \frac{1}{3 x - 1} = \frac{5}{6 x - 2}$ ．

查看试题解析
18. 分解因式：2m（m﹣n）²﹣8m²（n﹣m）

查看试题解析
19. 先化简，再求值： $(x + 2 - \frac{5}{x - 2}) \div \frac{x - 3}{3 x^{2} - 6 x}$ ，其中 $x$ 满足 $x^{2} + 3 x - 1 = 0$ .

查看试题解析
20. 如图，在平面直角坐标系xOy中，A（1，2），B（3，1），C（﹣2，﹣1）．

(1)、在图中作出△ABC关于x轴的对称图形△A₁B₁C₁ ．

(2)、写出点A₁ ， B₁ ， C₁的坐标（直接写答案）
A₁ B₁ C₁

(3)、求△ABC的面积．

查看试题解析
21. 在 $△ A B C$ 中， $A B = C B$ ， $∠ A B C = 90 °$ ， $F$ 为 $A B$ 延长线上一点，点 $E$ 在 $B C$ 上，且 $A E = C F$ ．

(1)、求证： $△ A B E ≌ △ C B F$ ；

(2)、若 $∠ C A E = 30 °$ ，求 $∠ A C F$ 度数．

查看试题解析
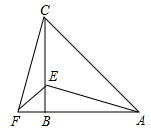22. “阅读陪伴成长，书香润泽人生．”某校为了开展学生阅读活动，计划从书店购进若干本A、B两类图书（每本A类图书的价格相同，每本B类图书的价格也相同），且每本A类图书的价格比每本B类图书的价格多5元，用1200元购进的A类图书与用900元购进的B类图书册数相同．

(1)、求每本A类图书和每本B类图书的价格各为多少元？

(2)、根据学校实际情况，需从书店一次性购买A、B两类图书共300册，购买时得知：一次性购买A、B两类图书超过100册时，A类图书九折优惠（B类图书按原价销售），若该校此次用于购买A、B两类图书的总费用不超过5100元，那么最多可以购买多少本A类图书？

查看试题解析
23.

(1)、如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE，则∠AEB的度数为．

(2)、如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE．求∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．

查看试题解析