安徽省铜陵市郊区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四组线段中，能组成三角形的是（）

A、2cm，3 cm，4 cm B、3 cm，4 cm，7 cm C、4 cm，6 cm，2 cm D、7 cm，10 cm，2 cm

查看试题解析
2. 下面运算结果为 $a^{6}$ 的是 $($ $)$

A、 $a^{3} + a^{3}$ B、 $a^{8} \div a^{2}$ C、 $a^{2} \cdot a^{3}$ D、 ${(- a^{2})}^{3}$

查看试题解析
3. 如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（）

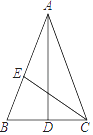A、20° B、35° C、40° D、70°

查看试题解析
4. 如图，在△ABC中，∠ABC＝75°，∠ABD＝∠BCD，则∠BDC的度数是（）

A、115° B、110° C、105° D、100°

查看试题解析
5. 如图所示，点E在△ABC外部，点D在BC边上，DE交AC于点F.若∠1＝∠2，∠E＝∠C，AE＝AC，则（）

A、△ABC≌△AFE B、△AFE≌△ADC C、△AFE≌△DFC D、△ABC≌△ADE

查看试题解析
6. 如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别是点D、E，AD=3，BE=1，则DE的长是（）

A、1.5 B、2 C、 $2 \sqrt{2}$ D、 $\sqrt{10}$

查看试题解析
7. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是（）

A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 $a (a - b) = a^{2} - a b$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
8. 化简 $\frac{x^{2} - x}{x + 1} \cdot \frac{x^{2} - 1}{x^{2} - 2 x + 1}$ 的结果是（）

A、 $\frac{1}{x}$ B、x C、 $\frac{x + 1}{x - 1}$ D、 $\frac{x - 1}{x + 1}$

查看试题解析
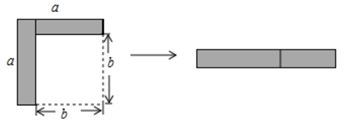9. 如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（）

A、4 B、5 C、6 D、7

查看试题解析
10. 如图，在等边△ABC中，BF是AC边上的中线，点D在BF上，连接AD，在AD的右侧作等边△ADE，连接EF，当△AEF周长最小时，∠CFE的大小是（）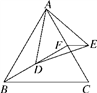

A、30° B、45° C、60° D、90°

查看试题解析

二、填空题

11. 等腰三角形一腰上的高与另一腰的夹角为30度，则它的底角的度数为

查看试题解析
12. 如果代数式m²+2m＝1，那么 $\frac{m^{2} + 4 m + 4}{m} \div \frac{m + 2}{m^{2}}$ 的值为．

查看试题解析
13. 方程 $\frac{2}{x + 2} = \frac{1}{x}$ 的解是．

查看试题解析
14. 观察下列算式： $3^{2} - 1^{2} = 8$ ， $5^{2} - 3^{2} = 16$ ， $7^{2} - 5^{2} = 24$ ， $9^{2} - 7^{2} = 32$ ，…，请将你发现的规律用式子表示出来：．

查看试题解析
15. 如图，直线 $B C$ 经过原点 $O$ ，点 $A$ 在 $x$ 轴上， $A D ⊥ B C$ 于 $D$ ．若A（4，0），B（m，3），C（n，-5），则 $A D \cdot B C =$ ．

查看试题解析

三、解答题

16. 分解因式：

(1)、 $6 x y^{2} - 9 x^{2} y - y^{3}$ ；

(2)、 $16 x^{4} - 1$

查看试题解析
17. 计算

(1)、 ${(- \frac{1}{3} a b^{2})}^{2} \cdot 27 a^{2} b \div (- 6 a^{3} b^{3})$ ；

(2)、 $(2 a - b) (3 a + 2 b) - b (a + b)$ ．

查看试题解析
18. 已知两个多边形的所有内角的和为1800°，且两个多边形的边数之比为2：5，求这两个多边形的边数.

查看试题解析
19. 已知（x³+mx+n）（x²﹣3x+1）展开后的结果中不含x³、x²项．求m+n的值．

查看试题解析
20. 已知a+b=7，ab=11，求代数式 $\frac{1}{2} a^{2} - \frac{1}{2} (a - b) b$ 的值．

查看试题解析
21. 甲、乙两个工程队计划修建一条长15千米的乡村公路，已知甲工程队每天比乙工程队每天多修路0.5千米，乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍．

(1)、求甲、乙两个工程队每天各修路多少千米？

(2)、若甲工程队每天的修路费用为0.5万元，乙工程队每天的修路费用为0.4万元，要使两个工程队修路总费用不超过5.2万元，甲工程队至少修路多少天？

查看试题解析
22. 已知，△ABC是等腰直角三角形，BC=AB，A点在x负半轴上，直角顶点B在y轴上，点C在x轴上方．

(1)、如图1所示，若A的坐标是（-3，0），点B的坐标是（0，1），求点C的坐标；

(2)、如图2，过点C作CD⊥y轴于D，请写出线段OA，OD，CD之间等量关系并说明理由；

(3)、如图3，若x轴恰好平分∠BAC，BC与x轴交于点E，过点C作CF⊥x轴于F，问CF与AE有怎样的数量关系？并说明理由．

查看试题解析