安徽省桐城市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图形分别是可回收垃圾、其它垃圾、厨余垃圾、有害垃圾标志，在这四个标志中，是轴对称图形的是（）.

A、 B、 C、 D、

查看试题解析
2. 若点A（﹣2，n）在x轴上，则点（n+1，n﹣3）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列命题中，属于真命题的是（）

A、一个三角形至少有两个内角是锐角 B、一个角的补角大于这个角 C、内错角相等 D、相等的角是对顶角

查看试题解析
4. 如图，用直尺和圆规作一个角的平分线，是运用了“全等三角形对应角相等”这一性质，由作图所得条件，判定三角形全等运用的方法是（）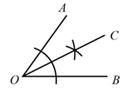

A、SAS B、ASA C、AAS D、SSS

查看试题解析
5. 已知一次函数 $y_{1} = a x + b$ 和 $y_{2} = b x + a$ （ $a b \neq 0$ 且 $a \neq b$ ），这两个函数的图象可能是（）

A、 B、 C、 D、

查看试题解析
6. 如图，已知 $△ A B C ≌ △ D E F$ ， $C D$ 平分 $∠ B C A$ ，若 $∠ D = 30 °$ ， $∠ C G F = 88 °$ ，则 $∠ E$ 的度数是（）

A、50° B、44° C、34° D、30°

查看试题解析
7. 如图， $C D$ 是等腰三角形 $△ A B C$ 底边 $A B$ 上的中线， $B E$ 平分 $∠ A B C$ ，交 $C D$ 于点 $E$ ， $A C = 6$ ， $D E = 2$ ，则 $△ B C E$ 的面积是（）

A、4 B、6 C、8 D、12

查看试题解析
8. 如图，等边 $△ A B C$ 中， $A B = 4$ ，点 $P$ 在边 $A B$ 上， $P D ⊥ B C$ ， $D E ⊥ A C$ ，垂足分别为 $D$ 、 $E$ ，设 $P A = x$ ，若用含 $x$ 的式子表示 $A E$ 的长，正确的是（）

A、 $2 - \frac{1}{2} x$ B、 $1 + \frac{1}{2} x$ C、 $3 - \frac{1}{4} x$ D、 $2 + \frac{1}{4} x$

查看试题解析
9. 如图， $A D$ 平分 $∠ B A C$ ， $D E ⊥ A C$ ，垂足为 $E$ ， $B F / / A C$ 交 $E D$ 的延长线于点 $F$ ，若 $B C$ 恰好平分 $∠ A B F$ ．则下列结论中：
① $A D$ 是 $Δ A B C$ 的高；

② $A D$ 是 $Δ A B C$ 的中线；

③ $E D = F D$ ；

④ $A B = A E + B F$ ．

其中正确的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完．假设每分钟的进水量和出水量是两个常数，容器内的水量 $y$ （单位：升）与时间 $x$ （单位：分）之间的部分关系如图所示．下列说法错误的是（）

A、每分钟的进水量为5升 B、每分钟的出水量为3.75升 C、从计时开始8分钟时，容器内的水量为25升 D、容器从进水开始到水全部放完的时间是21分钟

查看试题解析

二、填空题

11. 如图，已知 $∠ A B C = ∠ D C B$ ，则需添加的一个条件是可使 $△ A C B ≌ △ D B C$ .（只写一个即可，不添加辅助线）.

查看试题解析
12. 已知等腰三角形的一边长等于 $4 cm$ ，一边长等于 $9 cm$ ，它的周长为．

查看试题解析
13. 如图，一次函数 $y = \frac{3}{4} x + 6$ 的图象与x轴，y轴分交于点A，B，过点B的直线平分△ABO的面积，则直线l相应的函数表达式为．

查看试题解析

三、解答题

14. 如图，在 $△ A B C$ 中， $A B$ ， $A C$ 的垂直平分线分别交 $B C$ 于 $D$ ， $E$ ，垂足分别是 $M$ ， $N$ ．

(1)、若 $∠ B A C = 100 °$ ，则 $∠ D A E =$ ．

(2)、若 $∠ B A C = α$ （ $α > 90 °$ ），则 $∠ D A E =$ ．（用含α的式子表示）

查看试题解析
15. 如图，点 $A$ ， $B$ ， $C$ 都落在网格的格点上．

(1)、写出点 $A$ ， $B$ ， $C$ 的坐标；

(2)、求 $△ A B C$ 的面积：

(3)、把 $△ A B C$ 先向左平移4个单位长度，再向下平移5个单位长度，得 $△ A^{'} B^{'} C^{'}$ ，画出 $△ A^{'} B^{'} C^{'}$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A B$ 的垂直平分线交 $A B$ 于 $M$ ，交 $A C$ 于 $N$ ．

(1)、若 $∠ A B C = 70 °$ ，求 $∠ A$ 的度数；

(2)、连接 $N B$ ，若 $A B = 8 cm$ ， $△ N B C$ 的周长是 $14 cm$ ，求 $B C$ 的长．

查看试题解析
17. 在平面直角坐标系中，直线 $I_{1}$ ： $y_{1} = k_{1} x + b_{1}$ 与 $x$ 轴交于点 $B (12 ， 0)$ ，与直线 $I_{2}$ ： $y_{2} = k_{2} x$ 交于点 $A (6 ， 3)$ ．

(1)、分别求出直线 $I_{1}$ 和直线 $I_{2}$ 的表达式；

(2)、直接写出不等式 $k_{1} x + b_{1} < k_{2} x$ 解集．

查看试题解析
18. 如图，在△ABC中，∠B＝30°，∠C＝40°.

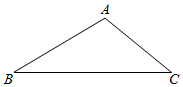(1)、尺规作图：①作边AB的垂直平分线交BC于点D；
②连接AD，作∠CAD的平分线交BC于点E；（要求：保留作图痕迹，不写作法）

(2)、在（1）所作的图中，求∠DAE的度数.

查看试题解析
19. 如图，有以下四个条件：①AC∥DE，②DC∥EF，③CD平分∠BCA，④EF平分∠BED．

(1)、若CD平分∠BCA，AC∥DE，DC∥EF，求证：EF平分∠BED．

(2)、除（1）外，请再选择四个条件中的三个作为题设，余下的一个作为结论，写出一个真命题，再给予证明．

查看试题解析
20. 已知 $△ A B C$ 和 $△ A D E$ 均为等腰三角形，且 $∠ B A C = ∠ D A E$ ， $A B = A C$ ， $A D = A E$ ．

(1)、如图1，点 $E$ 在 $B C$ 上，求证： $B C = B D + B E$ ；

(2)、如图2，点 $E$ 在 $C B$ 的延长线上，写出 $B C$ ， $B D$ ， $B E$ 的数量关系，并说明理由，

查看试题解析
21. 近年来，随着经济的发展和城镇化建设的推进，城市“停车难”问题越来越突出，某市为缓解城市“停车难”问题，市内某公共停车场执行新的计时收费标准是：停车不超过30分钟，不收费；超过30分钟，不超过60分钟，计1小时，收费3元；超过1小时后，超过1小时的部分按每小时2元收费（不足1小时，按1小时计）.

(1)、填空：张先生某次在该公共停车场停车2小时30分钟，应交停车费元；

(2)、填空：李先生也在该公共停车场停车，支付停车费11元，则停车场按小时（填整数）计时收费；

(3)、当x取正整数时，求该停车场停车费y（单位：元）关于停车计时x（单位：小时）的函数表达式.

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B > A C$ ， $∠ B = 45 °$ ，点 $D$ 是 $B C$ 边上一点，且 $A D = A C$ ，过点 $C$ 作 $C F ⊥ A D$ 于点 $E$ ，与 $A B$ 交于点 $F$ ．

(1)、若 $∠ C A D = α$ ，求 $∠ B C F$ 的度数（用含 $α$ 的式子表示）；

(2)、求证： $C A = C F$ ．

查看试题解析
23. 如图，点 $O$ 是等边 $△ A B C$ 内一点， $D$ 是 $△ A B C$ 外的一点， $∠ A O B = 110 °$ ， $∠ B O C = α$ ， $△ B O C ≌ △ A D C$ ， $∠ O C D = 60 °$ ，连接 $O D$ ．

(1)、求证： $Δ O C D$ 是等边三角形；

(2)、当 $α = 150 °$ 时，试判断 $△ A O D$ 的形状，并说明理由：

(3)、探究：当 $α$ 为多少度时， $O D = A D$ ？

查看试题解析