安徽省六安市金寨县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下图所示是我国四大银行的行标图案,其中是轴对称图形而不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的各组线段能组成三角形的是( )A、3cm、5cm、8cm B、5cm、6cm、12cm C、5cm、5cm、10cm D、7cm、 10cm、15cm3. 在平面直角坐标系中,若点P(-3,-1)向右平移4个单位得到点Q,则点Q在( )A、第四象限 B、第三象限 C、第二象限 D、第一象限4. 一次函数y=-3x-2的图象和性质,表述正确的是( )A、y 随x 的增大而增大 B、函数图象不经过第一象限 C、在y轴上的截距为2 D、与x轴交于点(-2,0)5. 如图所示,在下列条件中,不能判断 ≌ 的条件是( )
2. 下列长度的各组线段能组成三角形的是( )A、3cm、5cm、8cm B、5cm、6cm、12cm C、5cm、5cm、10cm D、7cm、 10cm、15cm3. 在平面直角坐标系中,若点P(-3,-1)向右平移4个单位得到点Q,则点Q在( )A、第四象限 B、第三象限 C、第二象限 D、第一象限4. 一次函数y=-3x-2的图象和性质,表述正确的是( )A、y 随x 的增大而增大 B、函数图象不经过第一象限 C、在y轴上的截距为2 D、与x轴交于点(-2,0)5. 如图所示,在下列条件中,不能判断 ≌ 的条件是( ) A、 , B、 , C、 , D、 ,6. 一副三角板如图叠放在一起,则∠α的度数是( )
A、 , B、 , C、 , D、 ,6. 一副三角板如图叠放在一起,则∠α的度数是( ) A、120° B、135° C、165° D、170°7. 下列命题中,真命题是( )A、三角形的一个外角大于任何一个内角 B、三角形的三条高所在直线一定相交于三角形内 C、有一个角是60°的三角形是等边三角形 D、三角形三条内角平分线相交于一点,这点到三角形三边的距离相等8. 如图,函数y=ax+4和y=2x的图象相交于点A(1,m),则不等式ax+4>2x的解集为( )
A、120° B、135° C、165° D、170°7. 下列命题中,真命题是( )A、三角形的一个外角大于任何一个内角 B、三角形的三条高所在直线一定相交于三角形内 C、有一个角是60°的三角形是等边三角形 D、三角形三条内角平分线相交于一点,这点到三角形三边的距离相等8. 如图,函数y=ax+4和y=2x的图象相交于点A(1,m),则不等式ax+4>2x的解集为( ) A、x>1 B、x<1 C、x>2 D、x<29. 14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图是 ( )
A、x>1 B、x<1 C、x>2 D、x<29. 14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图是 ( ) A、
A、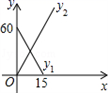 B、
B、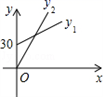 C、
C、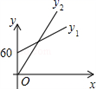 D、
D、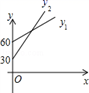 10. 如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点 A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为( )s时,△APQ是直角三角形.
10. 如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点 A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为( )s时,△APQ是直角三角形. A、2.4 B、3 C、2.4或3 D、3或4.8
A、2.4 B、3 C、2.4或3 D、3或4.8二、填空题
-
11. 函数 中自变量x的取值范围是 .12. 如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E,若AB=4,AC=6,则△ABD的周长为
 13. 在△ABC中,∠A=∠B= ∠C,则∠C 的度数为14. 如图,在△ABC中,∠BAC的平分线交BC于点D,过点D作DE⊥AC,DF⊥AB,垂足分别为E、F,下面四个结论:①∠AFE=∠AEF;②AD垂直平分EF;③ ;④EF//BC;一定成立的结论是(请将正确结论的序号填在横线上)
13. 在△ABC中,∠A=∠B= ∠C,则∠C 的度数为14. 如图,在△ABC中,∠BAC的平分线交BC于点D,过点D作DE⊥AC,DF⊥AB,垂足分别为E、F,下面四个结论:①∠AFE=∠AEF;②AD垂直平分EF;③ ;④EF//BC;一定成立的结论是(请将正确结论的序号填在横线上)
三、解答题
-
15. 如图,△ABC在平而直角坐标系中,其中A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
 (1)、作△ABC关于y轴对称的△A1B1C1 , 其中点A、B、C的对应点分别为A1 , B1 , C1;(2)、点P在x轴上,当PA+PC的值最小时,请在图中标出点P.16. 已知y与x-1成正比例,并且当x=3时,y=-4.(1)、求y与x之间的函数关系式;(2)、如果函数图象经过点P(m,6),求m的值.17. 如图所示,结合表格中的数据回答问题:
(1)、作△ABC关于y轴对称的△A1B1C1 , 其中点A、B、C的对应点分别为A1 , B1 , C1;(2)、点P在x轴上,当PA+PC的值最小时,请在图中标出点P.16. 已知y与x-1成正比例,并且当x=3时,y=-4.(1)、求y与x之间的函数关系式;(2)、如果函数图象经过点P(m,6),求m的值.17. 如图所示,结合表格中的数据回答问题:
梯形个数
1
2
3
4
5
…
图形周长
5
8
11
14
17
…
(1)、设图形的周长为I,梯形的个数为n,试写出I与n的函数解析式:(2)、求当n=11时,图形的周长.18. 如图,在△ABC中,AE是BC边上的高. (1)、若AD是边BC上的中线,AE=5cm,S△ABC=30cm²,求DC的长;(2)、若AD是∠BAC的平分线,∠B=30°,∠C=60°,求∠DAE的度数.19. 如图,直线y=kx+5经过点B(2,9)和A(-6,m)
(1)、若AD是边BC上的中线,AE=5cm,S△ABC=30cm²,求DC的长;(2)、若AD是∠BAC的平分线,∠B=30°,∠C=60°,求∠DAE的度数.19. 如图,直线y=kx+5经过点B(2,9)和A(-6,m) (1)、求k,m的值;(2)、直线AB与x轴交点为C,求△BOC的面积.20. 如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)、求k,m的值;(2)、直线AB与x轴交点为C,求△BOC的面积.20. 如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F. (1)、当DE=9,BC=5时,线段 AE的长为 ,(2)、已知∠D=35°,∠C=60°,求∠AFD的度数.21. 如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.
(1)、当DE=9,BC=5时,线段 AE的长为 ,(2)、已知∠D=35°,∠C=60°,求∠AFD的度数.21. 如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.
求证:
(1)、△ABC≌△AED;(2)、OB=OE.22. 某小区为了绿化环境,计划分两次购进A,B两种树苗,第一次购进A种树苗30棵,B种树苗15棵,共花费1350元;第二次购进A种树苗24棵,B种树苗10棵,共花费1060元.(两次购进的A,B两种树苗各自的单价均不变)(1)、A,B两种树苗每棵的价格分别是多少元?(2)、若购买A,B两种树苗共42棵,总费用为W元,购买A种树苗t棵,B种树苗的数量不超过A种树苗数量的2倍.求W与t的函数关系式.请设计出最省钱的购买方案,并求出此方案的总费用.23. 如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M. (1)、求证:BE=AD;(2)、用含α的式子表示∠AMB的度数.(3)、当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.
(1)、求证:BE=AD;(2)、用含α的式子表示∠AMB的度数.(3)、当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.