安徽省淮南市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $P (2020 ， - 2021)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列手机手势解锁图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 已知 $△ A B C ≌ △ D E F$ ，根据图中信息，得 $x =$ （）

A、15 B、18 C、20 D、25

查看试题解析
4. 如图， $△ A B C$ 中， $B C$ 边上的高是（）

A、 $A E$ B、 $A D$ C、 $C D$ D、 $C F$

查看试题解析
5. 等腰三角形的一个角为50°，则这个等腰三角形的顶角可能为（）

A、50° B、65° C、80° D、50°或80°

查看试题解析
6. 判断命题“如果 $0 < n < 1$ ，那么 $n^{2} - 1 > 0$ ”是假命题，只需举出一个反例，反例中n的值可以是（）．

A、 $- 2$ B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、 $2$

查看试题解析
7. 如图， $A$ 、 $B$ 的坐标分别为 $(1 ， 0)$ 、 $(0 ， 2)$ ，若将线段 $A B$ 平移到至 $A_{1} B_{1}$ ， $A_{1}$ 的坐标为 $(2 ， 1)$ ，则 $B_{1}$ 的坐标为（）

A、 $(1 ， 2)$ B、 $(1 ， 3)$ C、 $(0 ， 3)$ D、 $(2 ， 3)$

查看试题解析
8. 一次函数 $y_{1} = k_{1} x + b_{1}$ 的图象 $l_{1}$ 如图所示，将直线 $l_{1}$ 向下平移若干个单位后得直线 $l_{2}$ ， $l_{2}$ 的函数表达式为 $y_{2} = k_{2} x + b_{2}$ ．下列说法中错误的是（）

A、 $k_{1} = k_{2}$ B、 $b_{1} > b_{2}$ C、 $k_{1} > k_{2}$ D、当 $x = 5$ 时， $y_{1} > y_{2}$

查看试题解析
9. 已知 $A_{1} 、 A_{2} 、 A_{3} \dots \dots A_{n}$ 中， $A_{1}$ 与 $A_{2}$ 关于 $x$ 轴对称， $A_{2}$ 与 $A_{3}$ 关于 $y$ 轴对称， $A_{3}$ 与 $A_{4}$ 关于 $x$ 轴对称， $A_{4}$ 与 $A_{5}$ 关于 $y$ 轴对称……，如果 $A_{1}$ 在第二象限，那么 $A_{100}$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 已知直线 $l$ 及直线 $l$ 外一点 $D$ ，要求利用尺规作图过 $D$ 点作直线 $l$ 的平行线．对如图所示的两种作法，下列说法正确的是（）

A、两种作法都正确 B、两种作法都错误 C、左边作法正确，右边作法错误 D、右边作法正确，左边作法错误

查看试题解析

二、填空题

11. 函数 $y = \frac{5}{x - 3}$ 中自变量x的取值范围是．

查看试题解析
12. 小华要从长度分别为5cm，6cm，11cm，16cm的四根小木棒中选出三根摆成一个三角形，那么他选的三根木棒形成的三角形的周长为cm.

查看试题解析
13. 点 $(- \frac{1}{2} ， m)$ 和点 $(2 ， n)$ 在直线 $y = 2 x + b$ 上，则m与n的大小关系是．

查看试题解析
14. 如图，BD垂直平分线段AC，AE⊥BC，垂足为E，交BD于P点，AE＝7cm，AP＝4cm，则P点到直线AB的距离是．

查看试题解析

三、解答题

15. 如图，已知长方形ABCD的长为6，宽为4，请建立适当的平面直角坐标系，分别表示其各个顶点的坐标．

查看试题解析
16. 如图，点B、E、C、F在同一直线上，AB=DE，AC=DF，BE=CF．求证：∠A=∠D．

查看试题解析
17. 已知 $y$ 与 $3 x + 1$ 成正比例，且 $x = 2$ 时， $y = - 14$ ．

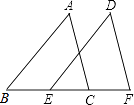(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、若点 $(a ， 2)$ 在这个函数的图象上，求 $a$ 的值．

查看试题解析
18. 如图，在平面直角坐标系中有 $△ A B C$ ：

⑴已知 $△ A_{1} B_{1} C_{1}$ 和 $△ A B C$ 关于 $y$ 轴对称，在图中画出 $△ A_{1} B_{1} C_{1}$ ；

⑵将 $△ A_{1} B_{1} C_{1}$ 沿 $x$ 轴向右平移4个单位，在图中画出平移后的 $△ A_{2} B_{2} C_{2}$ ；

⑶ $△ A_{2} B_{2} C_{2}$ 和 $△ A B C$ 关于某条直线 $l$ 对称，在图中画出对称轴 $l$ ．

查看试题解析
19. 为迎接新年，某单位组织员工开展娱乐竞赛活动，工会计划购进A、B两种电器共21件作为奖品.已知A种电器每件90元，B种电器每件70.设购买B种电器x件，购买两种电器所需费用为y元.

(1)、y与x的函数关系式为：

(2)、若购买B种电器的数量少于A种电器的数量，请给出一种最省费用的方案，并求出该方案所需费用.

查看试题解析
20. 如图， $△$ ABC的外角∠DAC的平分线交BC边的垂直平分线于P点，PD⊥AB于D，PE⊥AC于E．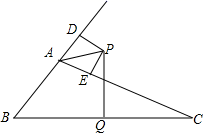

(1)、求证：BD＝CE；

(2)、若AB＝6cm，AC＝10cm，求AD的长．

查看试题解析
21. 如图，在平面直角坐标系中，直线 $y_{1} = - x + m$ 经过点 $B (2 ， 0)$ ，直线 $y_{2} = k x + b$ 经过点 $A (1 ， 0)$ 且与直线 $y_{1}$ 相交于点 $P (- 1 ， n)$ ．

(1)、 $m =$ ， $n =$ ；

(2)、求直线 $y_{2}$ 的解析式；

(3)、请把图象中直线 $y_{1} = - x + m$ 在直线 $y_{2} = k x + b$ 上方的部分描黑加粗，并直接写出不等式 $- x + m \geq k x + b$ 的解集．

查看试题解析
22. 在等边 $△ A B C$ 中， $D 、 E$ 分别为 $A B 、 A C$ 边上的动点，以 $D E$ 为一边作等边 $△ D E F$ ．

(1)、如图1，若等边 $△ D E F$ 的顶点 $F$ 恰好在 $B C$ 上，求证： $△ A D E ≌ △ C E F$ ；

(2)、如图2，若 $B D = 2 A E$ ，当点 $D$ 从点 $A$ 向点 $B$ 运动（不运动到点 $B$ ）时，连接 $C F$ ，请判断 $∠ E C F$ 的大小是否变化并说明理由．

查看试题解析