安徽省淮北市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $P (- 2 ， 3)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在函数 $y = \frac{1 - \sqrt{x}}{x - 2}$ 中，自变量 $x$ 的取值范围是（）

A、 $x \geq 0$ B、 $x \neq 2$ C、 $x \geq 0$ 且 $x \neq 2$ D、 $0 \leq x \leq 2$

查看试题解析
3. 以下列长度的各组线段为边，能组成三角形的是（）

A、 $1 cm$ ， $2 cm$ ， $3 cm$ B、 $2 cm$ ， $3 cm$ ， $5 cm$ C、 $5 cm$ ， $6 cm$ ， $12 cm$ D、 $4 cm$ ， $6 cm$ ， $8 cm$

查看试题解析
4. 小明在镜中看到身后墙上的时钟，实际时间最接近8时的是下图中的（）

A、 B、 C、 D、

查看试题解析
5. 点 $P (1 ， a)$ 和点 $Q (- 2 ， b)$ 都在正比例函数 $y = - 2 x$ 的图象上，则下列判断正确的是（）

A、 $a < b$ B、 $a \leq b$ C、 $a > b$ D、 $a \geq b$

查看试题解析
6. 如果点 $A (m ， 2)$ 和点 $B (3 ， n)$ 关于 $y$ 轴对称，则 $m$ 、 $n$ 的值为（）

A、 $m = - 3$ ， $n = - 2$ B、 $m = - 3$ ， $n = 2$ C、 $m = 3$ ， $n = 2$ D、 $m = 3$ ， $n = - 2$

查看试题解析
7. 甲、乙两人准备在一段长为1200米的笔直公路上进行跑步，甲、乙跑步的速度分别为4m/s和6m/s，起跑前乙在起点，甲在乙前面100米处，若同时起跑，则两人从起跑至其中一人先到达终点的过程中，甲、乙两之间的距离y（m）与时间t（s）的函数图象是（）

A、 B、 C、 D、

查看试题解析
8. 如图所示， $P$ 为 $△ A B C$ 外部一点， $D$ 、 $E$ 分别在 $A B$ 、 $A C$ 的延长线上，若点 $P$ 到 $B C$ 、 $B D$ 、 $C E$ 的距离都相等，则关于点 $P$ 的说法最佳的是（）

A、在 $∠ D B C$ 的平分线上 B、在 $∠ B C E$ 的平分线上 C、在 $∠ B A C$ 的平分线上 D、在 $∠ D B C$ 、 $∠ B C E$ 、 $∠ B A C$ 的平分线上

查看试题解析
9. 如图所示，函数 $y_{1} = | x |$ 和 $y_{2} = \frac{1}{3} x + \frac{4}{3}$ 的图像相交于 $(- 1 ， 1)$ ， $(2 ， 2)$ 两点，当 $y_{1} > y_{2}$ 时， $x$ 的取值范围是（）

A、 $x < - 1$ B、 $- 1 < x < 2$ C、 $x < - 1$ 或 $x > 2$ D、 $x > 2$

查看试题解析
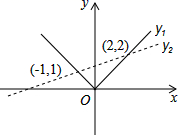10. 小明把一副含 $45 °$ ， $30 °$ 角的直角三角板按如图所示的方式摆放，其中 $∠ C = ∠ F = 90 °$ ， $∠ A = 45 °$ ， $∠ D = 30 °$ ，则 $∠ α + ∠ β$ 等于（）

A、 $180 °$ B、 $210 °$ C、 $270 °$ D、 $360 °$

查看试题解析

二、填空题

11. 命题：“任意两个奇数之和是偶数”的逆命题是命题．（填“真”或“假”）．

查看试题解析
12. 如图所示，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔4海里的A处，该海轮沿南偏东30°方向航行海里后，到达位于灯塔P的正东方向的B处．

查看试题解析
13. 若直线 $y = k x + b$ 与 $x$ 轴的交点坐标为 $(- 3 ， 0) ，$ 则关于 $x$ 的方程 $k x + b = 0$ 的解是．

查看试题解析
14. 如图，等腰三角形 $A B C$ 的底边 $B C$ 长为4，面积是12，腰 $A B$ 的垂直平分线 $E F$ 分别交 $A B$ ， $A C$ 于点 $E$ 、 $F$ ，若点 $D$ 为底边 $B C$ 的中点，点 $M$ 为线段 $E F$ 上一动点，则 $△ B D M$ 的周长的最小值为．

查看试题解析
15. 在平面直角坐标系中，点 $P (x ， y)$ 经过某种变换后得到点 $P^{'} (- y + 1 ， x + 2)$ ，我们把点 $P^{'} (- y + 1 ， x + 2)$ 叫做点 $P (x ， y)$ 的终结点．已知点 $P_{1}$ 的终结点为 $P_{2}$ ，点 $P_{2}$ 的终结点为 $P_{3}$ ，点 $P_{3}$ 的终结点为 $P_{4}$ ，这样依次得到 $P_{1}$ 、 $P_{2}$ 、 $P_{3}$ 、 $P_{4}$ 、… $P_{n}$ ，若点 $P_{1}$ 的坐标为 $(1 ， 0)$ ，则点 $P_{2021}$ 的坐标为．

查看试题解析

三、解答题

16. 已知一次函数 $y = k x + b (k \neq 0)$ 的自变量 $x$ 与函数 $y$ 之间的部分对应值如下表：

$x$

1

2

3

…

$y$

1

-1

-3

…

求这个一次函数的解析式．

查看试题解析
17. 在边长为1的小正方形网格中， $△ A O B$ 的顶点均在格点上．

(1)、 $B$ 点关于直线 $y = 1$ 对称的点的坐标为；

(2)、将 $△ A O B$ 向左平移3个单位长度，再向上平移2个单位长度得到 $△ A_{1} O_{1} B_{1}$ ，请画出 $△ A_{1} O_{1} B_{1}$ ；

(3)、在（2）的条件下， $△ A O B$ 边 $A B$ 上有一点 $P$ 的坐标为 $(a ， b)$ ，则平移后对应点 $P_{1}$ 的坐标为．

查看试题解析
18. 课间，小明拿着老师的等腰三角板玩，不小心掉在两墙之间，如图所示：

(1)、求证：△ADC≌△CEB；

(2)、已知DE=35cm，请你帮小明求出砌墙砖块的厚度a的大小（每块砖的厚度相同）

查看试题解析
19. 如图，在 $△ A B C$ 中，按以下步骤作图：①以 $B$ 为圆心，任意长为半径作弧，交 $A B$ 于 $D$ ，交 $B C$ 于 $E$ ；②分别以 $D$ ， $E$ 为圆心，以大于 $\frac{1}{2} D E$ 的同样长为半径作弧，两弧交于点 $F$ ；③作射线 $B F$ 交 $A C$ 于 $G$ ．如果 $A B = 6$ ， $B C = 8$ ， $△ A B G$ 的面积是15，求 $△ C B G$ 的面积．

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ A = ∠ A B C$ ，直线 $E F$ 分别交 $△ A B C$ 的边 $A B$ 、 $A C$ 和 $C B$ 的延长线于点 $D$ 、 $E$ 、 $F$ ．

(1)、若 $∠ A = 70 °$ ，则 $∠ F + ∠ F E C =$ ．

(2)、 $∠ F$ 、 $∠ F E C$ 、 $∠ A$ 有什么数量关系？请说明理由．

查看试题解析
21. 为便民惠民，树人公园特推出下列优惠方案：
①普通卡：每人每次20元；

②贵宾卡：年费为200元，每人每次10元；

③至尊卡：年费为500元，但进入不再收费．

设某人参观 $x$ 次时，所需总费用为 $y$ 元．

(1)、直接写出选择普通卡和贵宾卡消费时的函数关系式；

(2)、在同一个坐标系中，若三种方案对应的函数图象如图所示，求出点 $A$ ， $B$ ， $C$ 的坐标；

(3)、根据图象，直接写出选择哪种方案更合算．

查看试题解析
22. 在数学活动课上，数学老师出示了如下题目：
如图①，在四边形 $A B C D$ 中， $E$ 是边 $C D$ 的中点， $A E$ 是 $∠ B A D$ 的平分线， $A D ∥ B C$ ．

求证： $A B = A D + B C$ ．

小聪同学发现以下两种方法：

方法1：如图②，延长 $A E$ 、 $B C$ 交于点 $F$ ．

方法2：如图③，在 $A B$ 上取一点 $G$ ，使 $A G = A D$ ，连接 $E G$ 、 $C G$ ．

(1)、请你任选一种方法写出这道题的完整的证明过程；

(2)、如图④，在四边形 $A B C D$ 中， $A E$ 是 $∠ B A D$ 的平分线， $E$ 是边 $C D$ 的中点， $∠ B A D = 60 °$ ， $∠ D + \frac{1}{2} ∠ B C D = 180 °$ ，求证： $C B = C E$ ．

查看试题解析

$x$	1	2	3	…
$y$	1	-1	-3	…