安徽省合肥市庐阳区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列四个图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一个三角形三个内角的度数之比是2:3:4,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形4. 等腰三角形一边的长为 ,周长是 ,则底边的长是( )A、 B、 C、7或 D、4或5. 如图, 平分 , ,点 是 上的动点,若 ,则 的长可以是( )
3. 一个三角形三个内角的度数之比是2:3:4,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形4. 等腰三角形一边的长为 ,周长是 ,则底边的长是( )A、 B、 C、7或 D、4或5. 如图, 平分 , ,点 是 上的动点,若 ,则 的长可以是( ) A、 B、 C、 D、6. 一次函数 的图象经过两个点 和 ,则 , 的大小关系是( )A、 B、 C、当 时 D、当 时,7. 如图,直线 经过 中点 ,交 于点 ,交 于点 ,下列哪个条件不能使 ( )
A、 B、 C、 D、6. 一次函数 的图象经过两个点 和 ,则 , 的大小关系是( )A、 B、 C、当 时 D、当 时,7. 如图,直线 经过 中点 ,交 于点 ,交 于点 ,下列哪个条件不能使 ( ) A、 B、 C、 D、8. 一次函数 的图象与 轴交于点 ,将一次函数图象绕着点 转动,转动后得到的一次函数图象与两坐标轴所围成的面积比原来增加2,则转动后得到的一次函数图象与 轴交点横坐标为( )A、 B、3 C、3或 D、6或9. 如图, 为直角三角形, , ,点 、 分别在边 、 上,将 沿 折叠,点 恰好落在边 上的点 ,若 平分 , ,则 的长为( )
A、 B、 C、 D、8. 一次函数 的图象与 轴交于点 ,将一次函数图象绕着点 转动,转动后得到的一次函数图象与两坐标轴所围成的面积比原来增加2,则转动后得到的一次函数图象与 轴交点横坐标为( )A、 B、3 C、3或 D、6或9. 如图, 为直角三角形, , ,点 、 分别在边 、 上,将 沿 折叠,点 恰好落在边 上的点 ,若 平分 , ,则 的长为( ) A、4 B、5 C、6 D、810. 一次函数 和 在同一平面直角坐标系中的图象可能是( )A、
A、4 B、5 C、6 D、810. 一次函数 和 在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 函数 的自变量 的取值范围是 .12. “同旁内角互补,两直线平行”的逆命题是.13. 小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完;销售金额与卖西瓜千克数之间的关系如图所示,那么小李赚了.元.
 14. 如图,在 中, , , 是 的平分线,交 于点 , 是 的中点.连接 并延长,交 的延长线于点 ,连接 .写出图中三角形中所有的等腰三角形 .
14. 如图,在 中, , , 是 的平分线,交 于点 , 是 的中点.连接 并延长,交 的延长线于点 ,连接 .写出图中三角形中所有的等腰三角形 .
三、解答题
-
15. 中, , ,求三角形中各角的度数.16. 已知 是 的一次函数,且当 , ;当 时, .(1)、求这个一次函数的表达式:(2)、将该函数图象向下平移3个单位,求平移后图象的函数表达式.17. 如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系,已知三角形 的顶点 的坐标为 ,顶点 的坐标为 ,顶点 的坐标为 .
 (1)、把三角形 向下平移4个单位长度,再以 轴为对称轴对称,得到三角形 ,请你画出三角形 并直接写出点 , , 的坐标;(2)、求三角形 的面积.18. 如图, 中, , ,垂足为 , 是边 的垂直平分线,交 于 ,交 于点 ,求 的度数.
(1)、把三角形 向下平移4个单位长度,再以 轴为对称轴对称,得到三角形 ,请你画出三角形 并直接写出点 , , 的坐标;(2)、求三角形 的面积.18. 如图, 中, , ,垂足为 , 是边 的垂直平分线,交 于 ,交 于点 ,求 的度数. 19. 如图,一次函数 的图像与 轴交于点 ;一次函数 的图像与 轴交于点 ,且经过点 ,两函数图象交于点 .
19. 如图,一次函数 的图像与 轴交于点 ;一次函数 的图像与 轴交于点 ,且经过点 ,两函数图象交于点 .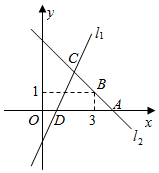 (1)、求 , , 的值;(2)、根据图象,直接写出 的解集.20. 如图,在 和 中, , , 与 的延长线交于点 .
(1)、求 , , 的值;(2)、根据图象,直接写出 的解集.20. 如图,在 和 中, , , 与 的延长线交于点 . (1)、求证: ;(2)、求证:21. 如图, , , ,动点 从点 出发,沿 轴以每秒1个单位长的速度向正方向移动,过点 的直线 也随之移动,设移动时间为t秒.
(1)、求证: ;(2)、求证:21. 如图, , , ,动点 从点 出发,沿 轴以每秒1个单位长的速度向正方向移动,过点 的直线 也随之移动,设移动时间为t秒. (1)、若直线 与线段 有交点,确定 的取值范围;(2)、设直线 与 轴交点为 ,若 取得最小值,求此时直线l的函数解析式.22.(1)、观察与发现
(1)、若直线 与线段 有交点,确定 的取值范围;(2)、设直线 与 轴交点为 ,若 取得最小值,求此时直线l的函数解析式.22.(1)、观察与发现小明将三角形纸片 沿过点 的直线折叠,使得 落在 边上,折痕为 ,展开纸片(如图①);再次折叠该三角形纸片,使点 和点 重合,折痕为 , 与 相交于点 ,展平纸片后得到 (如图②).小明认为 是等腰三角形,你同意吗?请说明理由.
 (2)、实践与运用
(2)、实践与运用将长方形纸片 沿过点 的直线折叠,使点 落在 边上的点 处,折痕为 (如图③);再沿过点 的直线折叠,使点落 在 上的点 处,折痕为 (如图④);再展平纸片(如图⑤).求图⑤中 的大小.
 23. 为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
23. 为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:车型 目的地 A村(元/辆) B村(元/辆) 大货车 800 900 小货车 400 600
(1)、求这15辆车中大小货车各多少辆?(2)、现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.(3)、在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.