安徽省合肥市庐江县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $a + a = a^{2}$ B、 $a^{2} \cdot a = a^{2}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(a^{3})}^{2} = a^{6}$

查看试题解析
3. 某种细胞的直径是0.00000095米，将0.00000095用科学记数法表示为（）

A、 $0.95 \times 10^{- 7}$ B、 $9.5 \times 10^{- 8}$ C、 $9.5 \times 10^{- 7}$ D、 $95 \times 10^{- 5}$

查看试题解析
4. 要使分式 $\frac{3}{x - 1}$ 有意义，则x的取值范围是（）

A、x≠1 B、x＞1 C、x＜1 D、x≠﹣1

查看试题解析
5. 用直尺和圆规作一个角等于已知角，如图，能得出 $∠ A O B = ∠ A^{'} O^{'} B^{'}$ 的依据是（）

A、 $SAS$ B、 $SSS$ C、 $ASA$ D、 $AAS$

查看试题解析
6. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽．“其大意为：现请人代买一批椽，这批椽的价钱为6210文．如果每件椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为 $x$ 株，则正确的方程是（）

A、 $3 (x - 1) = \frac{6210}{x}$ B、 $\frac{6210}{x - 1} = 3$ C、 $3 x - 1 = \frac{6210}{x}$ D、 $\frac{6210}{x} = 3$

查看试题解析
7. 如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（）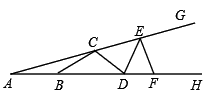

A、80° B、90° C、100° D、108°

查看试题解析
8. 如果 $x^{2} + (m - 2) x + 9$ 是个完全平方式，那么 $m$ 的值是（）

A、8 B、-4 C、±8 D、8或-4

查看试题解析
9. 已知关于x的分式方程 $\frac{x}{x - 2} - 4 = \frac{k}{2 - x}$ 的解为正数，则k的取值范围是（）

A、 $- 8 < k < 0$ B、 $k > - 8$ 且 $k \neq - 2$ C、 $k > - 8$ 且 $k \neq 2$ D、 $k < 4$ 且 $k \neq - 2$

查看试题解析
10. 如图，在 $△ O A B$ 和△ $O C D$ 中， $O A = O B$ ， $O C = O D$ ， $O A > O C$ ， $∠ A O B = ∠ C O D = 40 °$ ，连接AC，BD交于点M，连接OM．下列结论：

① $A C = B D$ ；② $∠ A M B = 40 °$ ；③OM平分 $∠ B O C$ ；④MO平分 $∠ B M C$ ．

其中一定正确的为（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

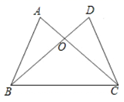
11. 若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是．

查看试题解析
12. 如图，已知 $A C = D B$ ，添加一个条件，可以得到 $△ A B C ≌ △ D C B$ ．

查看试题解析
13. 把多项式 $m^{2} n + 6 m n + 9 n$ 分解因式的结果是．

查看试题解析
14. 在 $Δ A B C$ 中， $A B = A C$ ， $A B$ 的垂直平分线与 $A C$ 所在的直线相交所得到的锐角为 $40^{\circ}$ ，则 $∠ B$ 等于度．

查看试题解析

三、解答题

15. 解方程： $\frac{1 - 2 x}{x - 3} = \frac{5}{3 - x} - 1$ ．

查看试题解析
16. 如图是A，B，C三岛的平面图，C岛在A岛的北偏东35°方向，B岛在A岛的北偏东80°方向，C岛在B岛的北偏西55°方向，问A，B，C三岛组成一个什么样的三角形，并说明理由．

查看试题解析
17. 已知 $5 x^{2} - x - 1 = 0$ ，求代数式 $(3 x + 2) (3 x - 2) + x (x - 2)$ 的值．

查看试题解析
18. 先化简，再求值． $(\frac{2 x - 1}{x + 1} - x + 1) \div \frac{x - 2}{x^{2} - 1}$ ，在 $0 < x < 4$ 范围中，选取合适的整数x代入求值．

查看试题解析
19. 如图，C是 $∠ A O B$ 内部的一条射线OM上一点，D、E分别在边OA、OB上． $C D = C E$ ， $∠ O D C + ∠ O E C = 180 °$ ．求证： $∠ A O M = ∠ B O M$ ．

查看试题解析
20. 如图，在平面直角坐标系中， $A (- 3 ， 2)$ ， $B (- 4 ， - 3)$ ， $C (- 1 ， - 1)$ ．

①在图中作出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ；

②求 $△ A_{1} B_{1} C_{1}$ 的面积；

③在y轴上确定点P，使 $△ P B C$ 周长最小．

查看试题解析
21. 图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

(1)、请写出图2中阴影部分的面积：；

(2)、观察图2，你能写出下列三个式子： ${(m + n)}^{2}$ ， ${(m - n)}^{2}$ ， $m n$ 之间的等量关系吗？

(3)、根据（2）中的等量关系，已知： $a - \frac{2}{a} = 1$ 求： $a + \frac{2}{a}$ 的值．

查看试题解析
22. 2016年12月29日，引江济淮工程正式开工．该工程供水范围涵盖安徽省12个市和河南省2个市，共55个区县．其中在我县一段工程招标时，有甲、乙两个工程队投标，从投标书上得知：甲队单独完成这项工程需要60天，若由甲队先做20天，剩下的工程由甲、乙合作24天可完成．

(1)、乙队单独完成这项工程需要多少天？

(2)、现将该工程分为两部分，甲队做完其中一部分工程用了m天，乙队做完其中一部分工程用了n天，m，n都是正整数，且甲队用时不到20天，乙队用时不到65天，甲队施工一天，需付工程款3.5万元，乙队施工一天需付工程款2万元．请用含m的式子表示n，并求出该工程款总共为多少万元？

查看试题解析
23. 在 $△ A B C$ 中， $A B = A C$ ， $C G ⊥ B A$ 交BA的延长线于点G．

(1)、将一等腰直角三角尺按图1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC重合，另一条直角边恰好经过点B．通过观察、测量BF与CG的长度，得到 $B F = C G$ ．请给予证明．

(2)、当三角尺沿AC方向移动到图2所示的位置时，一条直角边仍与AC边重合，另一条直角边交BC于点D，过点D作 $D E ⊥ B A$ 垂足为E．此时请你通过观察、测量DE，DF与CG的长度，猜想并写出DE、DF与CG之间存在的数量关系，并证明你的猜想．

(3)、当三角尺在图2的基础上沿AC方向继续移动到图3所示的位置（点F在线段AC上，且点F与点C不重合）时，请你判断（2）中的猜想是否仍然成立？（不用证明）

查看试题解析