安徽省合肥市肥东县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-27 类型:期末考试
一、单选题
-
1. 下面是科学防控新冠肺炎病毒传染的宣传图片,图片上有图案和文字说明,其中图案是轴对称图形的是( )A、
 打喷嚏 捂口鼻
B、
打喷嚏 捂口鼻
B、 喷嚏后 慎揉眼
C、
喷嚏后 慎揉眼
C、 勤洗手 勤通风
D、
勤洗手 勤通风
D、 戴口罩 讲卫生
2. 如果点 P(x,6)在第二象限,则 x 的取值范围是( )A、x>0 B、x<0 C、x≥0 D、x≤03. 下列4个函数关系:y=2x+1,y= ,s=60t,y=100﹣25x,其中是一次函数的共有( )A、1个 B、2个 C、3个 D、4个4. 对假命题“若 ,则 ”举反例,正确的反例是( )A、 B、 C、 D、5. 已知 是函数 图象上的两点,下列判断正确的是( )A、 B、 C、当 时, D、当 时,6. 用直尺和圆规作一个角等于已知角,如图,能得出 的依据是( )
戴口罩 讲卫生
2. 如果点 P(x,6)在第二象限,则 x 的取值范围是( )A、x>0 B、x<0 C、x≥0 D、x≤03. 下列4个函数关系:y=2x+1,y= ,s=60t,y=100﹣25x,其中是一次函数的共有( )A、1个 B、2个 C、3个 D、4个4. 对假命题“若 ,则 ”举反例,正确的反例是( )A、 B、 C、 D、5. 已知 是函数 图象上的两点,下列判断正确的是( )A、 B、 C、当 时, D、当 时,6. 用直尺和圆规作一个角等于已知角,如图,能得出 的依据是( ) A、 B、 C、 D、7. 已知直线 与直线 的交点坐标为 ,则关于 的不等式 的解集为( )A、 B、 C、 D、8. 如图, 为 的中线, 为 的中点,连接 .已知 的面积为12,则 的面积等于( )
A、 B、 C、 D、7. 已知直线 与直线 的交点坐标为 ,则关于 的不等式 的解集为( )A、 B、 C、 D、8. 如图, 为 的中线, 为 的中点,连接 .已知 的面积为12,则 的面积等于( )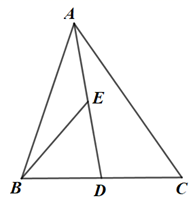 A、 B、 C、 D、9. 如图,点 是 平分线上的点,过点 作 交 于点 .若在边 上有一点N,且 ,则下列结论一定成立的是( )
A、 B、 C、 D、9. 如图,点 是 平分线上的点,过点 作 交 于点 .若在边 上有一点N,且 ,则下列结论一定成立的是( )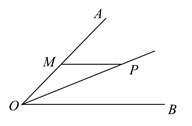 A、 B、 C、 D、10. 东东和爸爸一起往华中公园方向去旅游,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,东东继续前行,5分钟后也原路返回,两人恰好同时到家.东东和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论中错误的是( )
A、 B、 C、 D、10. 东东和爸爸一起往华中公园方向去旅游,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,东东继续前行,5分钟后也原路返回,两人恰好同时到家.东东和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论中错误的是( )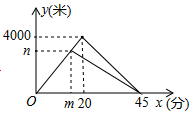 A、两人前行过程中的速度为200米/分 B、m的值是15,n的值是3000 C、东东开始返回时与爸爸相距1800米 D、运动18分钟或30分钟时,两人相距900米
A、两人前行过程中的速度为200米/分 B、m的值是15,n的值是3000 C、东东开始返回时与爸爸相距1800米 D、运动18分钟或30分钟时,两人相距900米二、填空题
-
11. 的三边长分别为 ,且 为整数,则 的值是 .12. 函数 中自变量 的取值范围是 .13. 如图,在 中, 分别垂直平分边 ,交 于点 ,如果 ,那么 的周长为 .
 14. 已知点 的坐标为 ,且点 到两坐标轴的距离相等,则 .15. 如图,在 中, ,在 上取一点 ,延长 到 ,使得 连接 .完成下列问题:(1)、 的度数等于度;(2)、如果继续在 上取一点 ,延长 到 ,使得 ,连接 ,……,依此进行下去,那么以 为顶点的锐角的度数等于度.
14. 已知点 的坐标为 ,且点 到两坐标轴的距离相等,则 .15. 如图,在 中, ,在 上取一点 ,延长 到 ,使得 连接 .完成下列问题:(1)、 的度数等于度;(2)、如果继续在 上取一点 ,延长 到 ,使得 ,连接 ,……,依此进行下去,那么以 为顶点的锐角的度数等于度.
三、解答题
-
16. 已知 与 成正比例,且当 时, .(1)、求出 与 之间的函数解析式;(2)、当 时,求 的值.17. 已知,在 网格中建立如图所示的平面直角坐标系, 是格点三角形(三角形的顶点是网格线的交点).

⑴画出 关于 轴对称的 ;
⑵画出 向下平移5个单位长度得到的 ;
⑶若点 的坐标为 ,请写出点 经过两次图形变换的对应点 的坐标.
18. 如图,在 中, 于点 于点 且 平分 . (1)、求 的度数;(2)、求 的度数.19. 如图,直线 与 轴交于点 ,与 轴交于点 ,它在 轴上的截距是 .
(1)、求 的度数;(2)、求 的度数.19. 如图,直线 与 轴交于点 ,与 轴交于点 ,它在 轴上的截距是 . (1)、求点 的坐标;(2)、若直线 上有一点 ,且 求点 的坐标20. 如图, 是等边三角形,延长 到 使 .点 是边 的中点,连接 并延长交 于 .
(1)、求点 的坐标;(2)、若直线 上有一点 ,且 求点 的坐标20. 如图, 是等边三角形,延长 到 使 .点 是边 的中点,连接 并延长交 于 . (1)、求 的度数;(2)、求证: .21. 工厂计划购进一种标价为 元/ 的原料 ,目前此原料促销,有两种优惠方式可供选择.方式一:购买总费用 (元)关于 的函数图象如图中 所示,其中 的坐标为 ;方式二:如果购买此原料不超过 ,则按标价销售,如果超过 ,则超出部分按八折销售.设选择方式二购买 时的总费用为 元.
(1)、求 的度数;(2)、求证: .21. 工厂计划购进一种标价为 元/ 的原料 ,目前此原料促销,有两种优惠方式可供选择.方式一:购买总费用 (元)关于 的函数图象如图中 所示,其中 的坐标为 ;方式二:如果购买此原料不超过 ,则按标价销售,如果超过 ,则超出部分按八折销售.设选择方式二购买 时的总费用为 元.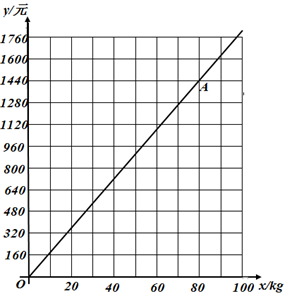 (1)、求 关于 的函数解析式;(2)、在图中画出 关于 的函数图象.结合图象回答:为了使购买总费用较少,如何选择优惠方式?请直接写出结果.22. 如图,已知 中, ,点 为 的中点.如果点 在线段 上以 的速度由点 向 点运动,同时,点 在线段 上由 点向 点运动,设点 运动的时间为 .
(1)、求 关于 的函数解析式;(2)、在图中画出 关于 的函数图象.结合图象回答:为了使购买总费用较少,如何选择优惠方式?请直接写出结果.22. 如图,已知 中, ,点 为 的中点.如果点 在线段 上以 的速度由点 向 点运动,同时,点 在线段 上由 点向 点运动,设点 运动的时间为 . (1)、用含 的式子表示 的长为;(2)、若点 的运动速度与点 的运动速度相等,经过 秒后, 与 是否全等?请说明理由;(3)、若点 的运动速度与点 的运动速度不相等,当点 的运动速度为多少时,能够使 与 全等?
(1)、用含 的式子表示 的长为;(2)、若点 的运动速度与点 的运动速度相等,经过 秒后, 与 是否全等?请说明理由;(3)、若点 的运动速度与点 的运动速度不相等,当点 的运动速度为多少时,能够使 与 全等?