安徽省合肥市包河区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 下面四个手机应用图标中是轴对称图形的是（　　）

    A、 B、 C、 D、

    查看试题解析

  • 2. 若正比例函数y＝- 12 x的图象经过点P（m，1），则m的值是（  ）
    A、-2 B、- 12 C、12 D、2

    查看试题解析

  • 3. 已知P是△ABC内一点，连接PA，PB，PC，且PA=PB=PC，则P点一定是（  ）
    A、△ABC的三条中线的交点 B、△ABC的三条内角平分线的交点 C、△ABC的三条高的交点 D、△ABC的三边的中垂线的交点

    查看试题解析

  • 4. 若点P是第二象限内的点，且点P到x轴的距离是4，到y轴的距离是5，则点P的坐标是（  ）
    A、（﹣4，5） B、（4，﹣5） C、（﹣5，4） D、（5，﹣4）

    查看试题解析

  • 5. 下列四组线段中，不可以构成三角形的是（  ）
    A、4，5，6 B、1.5，2，2.5 C、13 ， 14 ， 15 D、1， 2 ，3

    查看试题解析

  • 6. 直线kx-3y＝8，2x+5y＝-4交点的纵坐标为0，则k的值为（  ）
    A、4 B、﹣4 C、2 D、-2

    查看试题解析

  • 7.

    如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（　　）


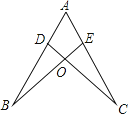    A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD

    查看试题解析

  • 8. 如图，CE是△ABC的外角∠ACD的平分线，若∠B＝35°，∠ACE＝60°，则∠A＝（  ）

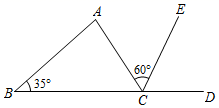    A、105° B、95° C、85° D、75°

    查看试题解析

  • 9. 如图，在四边形ABCD中，AC ， BD为对角线，AB＝BC＝AC＝BD ， 则∠ADC的大小为（ ）

    A、120° B、135° C、145° D、150°

    查看试题解析

  • 10. 如图，在平面直角坐标系中，半径为1个单位长度的半圆O1 ， O2 ， O3 ， …，组成一条平滑曲线，点P从点O出发，沿这条曲线向右运动，速度为每秒 π2 个单位长度，则第2020秒时，点P的坐标是（  ）

    A、（2020，-1） B、（2020，0） C、（2019，-1） D、（2019，0）

    查看试题解析

二、填空题

  • 11. 请写出命题“直角三角形的两个锐角互余”的逆命题： ．

    查看试题解析

  • 12. 如图，D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，若AB=4，CF=3，则BD= ．

    查看试题解析

  • 13. 如图，两个一次函数y＝kx+b与y＝mx+n的图象分别为直线l1和l2 ， l1与l2交于点A（1，p），l1与x轴交于点B（-2，0），l2与x轴交于点C（4，0），则不等式组0＜mx+n＜kx+b的解集为 ．

    查看试题解析

  • 14. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”小明的做法，其理论依据是

    查看试题解析

  • 15. 如图，在平面直角坐标系中，过点C（0，6）的直线AC与直线OA相交于点A（4，2），动点M在直线AC上，且△OMC的面积是△OAC的面积的 14 ，则点M的坐标为 ．

    查看试题解析

  • 16. 对于实数 a ， b ，我们定义符号 max{a ， b} 的意义为：当 a≥b 时， max{a ， b}=a ．当 a<b 时， max{a ， b}=b ；如： max{5 ， 5}=5 ， max{−3 ， 2} =2，若关于 x 的函数为 y=max{x+3 ， −x+1} ，则该函数的最小值为 ．

    查看试题解析

  • 17. 如图，已知△ABC中，AB＝AC，∠BAC＝90°，BF⊥AD垂足为E，连接DF，若S△ADF＝ 154 ，∠AFB＝∠CFD，则DF的长为 ．

    查看试题解析

三、解答题

  • 18. 如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）.

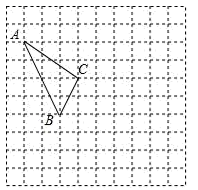    (1)、请在如图所示的网格平面内作出平面直角坐标系；
    (2)、请作出△ABC关于y轴对称的△A1B1C1；
    (3)、写出点B1的坐标；
    (4)、求△ABC的面积.

    查看试题解析

  • 19.        

     

    (1)、∠MAB为锐角，AB＝a，点C在射线AM上，点B到射线AM的距离为d，BC＝x，若△ABC的形状、大小是唯一确定的，则x的取值范围是 ．
    (2)、如图，∠MAB＝30°，AB＝2cm，点C在射线AM上，画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题，请画出图形，并写出你所选取的BC的长约为cm（精确到0.1cm）．

    查看试题解析

  • 20. 如图，在△ABC 中，已知点 D 在线段 AB 的反向延长线上，过 AC的中点 F 作线段 GE 交∠DAC 的平分线于 E，交 BC 于 G，且 AE∥BC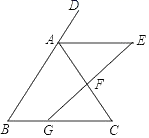

    (1)、求证：△ABC 是等腰三角形；
    (2)、若 AE=8，AB=10，GC=2BG，求△ABC 的周长．

    查看试题解析

  • 21. 周一早上8：00小明步行去学校，途中他在文具店停了2分钟，然后直达到学校，如图，是小明距学校的距离y（米）与他所用的时间x（分）之间的函数图象．请你根据以上信息，解答下列问题：

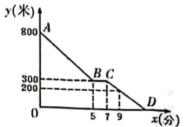    (1)、求线段AB所对应的函数关系式；
    (2)、已知小明离开文具店步行2分钟后，离学校还有200米，问小明几点几分到达学校？

    查看试题解析

  • 22. 在△ABC中，AB＝AC，在△ABC的外部作等边三角形△ACD．E为AC的中点，连接DE并延长交BC于点F，连接BD．

    (1)、如图1，若∠BAC＝100°，求∠BDF的度数；
    (2)、如图2，∠ACB的平分线交AB于点M，交EF于点N，连接BN．

    ①补全图2；

    ②若BN＝DN，求证：MB＝MN．

    查看试题解析