安徽省阜阳市颍州区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 以下四家银行的行标图中，是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 以下列各组线段为边，能组成三角形的是（）

A、2，3，5 B、2，3，6 C、8，6，4 D、6，7，14

查看试题解析
3. 要使分式 $\frac{x + 1}{x - 2}$ 有意义，则x的取值应满足（）

A、 $x \neq 2$ B、 $x \neq - 1$ C、 $x = 2$ D、 $x = - 1$

查看试题解析
4. 下列各式中能用平方差公式的是（）

A、(x＋y)(y＋x) B、（x＋y)(y－x) C、(x＋y)(－y－x) D、(－x＋y)(y－x)

查看试题解析
5. 如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）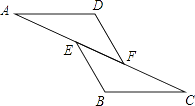

A、∠A=∠C B、AD=CB C、BE=DF D、AD∥BC

查看试题解析
6. 如果一个多边形的内角和为 $1260 °$ ，那么从这个多边形的一个顶点可以作（）条对角线．

A、 $4$ B、 $5$ C、 $6$ D、 $7$

查看试题解析
7. 在直角坐标系中，已知A（-3，3），在y轴上确定一点P ，使△AOP为等腰三角形，则符合条件的点P共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 下列命题中，真命题有（）
①有一个角为60°的三角形是等边三角形；②底边相等的两个等腰三角形全等；③有一个角是40°，腰相等的两个等腰三角形全等；④一边上的中线等于这条边的一半的三角形是直角三角形.

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 为推进垃圾分类，推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用 $360$ 万元购买甲型机器人和用 $480$ 万元购买乙型机器人的台数相同，两型号机器人的单价和为 $140$ 万元.若设甲型机器人每台 $x$ 万元，根据题意，所列方程正确的是（）

A、 $\frac{360}{x} = \frac{480}{140 - x}$ B、 $\frac{360}{140 - x} = \frac{480}{x}$ C、 $\frac{360}{x} + \frac{480}{x} = 140$ D、 $\frac{360}{x} - 140 = \frac{480}{x}$

查看试题解析
10. 如图， $△ ABC$ 中， $∠ BAC = 60 °$ ， $∠ BAC$ 的平分线 $A D$ 与边 $B C$ 的垂直平分线 $M D$ 相交于点 $D$ ， $D E ⊥ A B$ 交 $A B$ 的延长线于点 $E$ ， $D F ⊥ A C$ 于点 $F$ ，现有下列结论：① $D E = D F$ ；② $D E + D F = A D$ ；③ $D M$ 平分 $∠ A D F$ ；④ $A B + A C = 2 A E$ ．其中正确的有（）

A、①② B、①②③④ C、①②④ D、②④

查看试题解析

二、填空题

11. 分解因式： $a b^{3} - a^{3} b =$ ．

查看试题解析
12. 计算： $- 1^{4} + | - 3 | - {(- \frac{1}{2})}^{- 3} + {(2 - \sqrt{3})}^{0} =$ ．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 30 °$ ，分别以 $A$ ， $B$ 两点为圆心，大于 $\frac{1}{2} AB$ 为半径画弧，两弧交于 $M$ ， $N$ 两点，直线 $M N$ 交 $A C$ 于点 $D$ ，若 $C D = 4$ ，则 $A C$ 的长度为．

查看试题解析
14. 若 $x \neq - 1$ ，则把 $- \frac{1}{x + 1}$ 称为 $x$ 的“和 $1$ 负倒数”，如： $2$ 的“和 $1$ 负倒数”为 $- \frac{1}{3}$ ， $- 3$ 的“和 $1$ 负倒数”为 $\frac{1}{2}$ ，若 $x_{1} = \frac{2}{3}$ ， $x_{2}$ 是 $x_{1}$ 的“和 $1$ 负倒数”， $x_{3}$ 是 $x_{2}$ 的“和 $1$ 负倒数”，…依此类推，则 $x_{2020}$ 的值为．

查看试题解析

三、解答题

15. 计算：(x-y)²-(y+2x)( y-2x)．

查看试题解析
16. 解分式方程： $\frac{3}{2 x + 1} - \frac{2}{2 x - 1} = \frac{x + 1}{4 x^{2} - 1}$ .

查看试题解析
17. 先化简，再求值： $\frac{b^{2}}{a^{2} - a b} \div (\frac{a^{2} - b^{2}}{a^{2} - 2 a b + b^{2}} + \frac{a}{b - a})$ ，其中 $a = - 2$ ， $b = \frac{1}{3}$ ．

查看试题解析
18. 如图，点 $B$ ， $E$ ， $C$ ， $F$ 在一条直线上， $A B = D E$ ， $A C = D F$ ， $B E = C F$ ．

求证：

(1)、 $∠ A = ∠ D$ ；

(2)、 $A B // D E$ ．

查看试题解析
19. 如图，已知 $A (- 2 ， 4)$ $B (4 ， 2)$ ， $C (2 ， - 1)$ ，三点.

⑴作 $Δ A B C$ 关于 $x$ 轴的对称图形 $Δ A_{1} B_{1} C_{1}$ ，写出点 $C$ 关于 $x$ 轴的对称点 $C_{1}$ 的坐标；

⑵ $P$ 为 $x$ 轴上一点，请在图中找出使 $Δ P A B$ 的周长最小时的点 $P$ 并直接写出此时点 $P$ 的坐标（保留作图痕迹）.

查看试题解析
20. 列方程（组）解应用题：
为顺利通过国家义务教育均衡发展验收，我市某中学配备了两个多媒体教室，购买了笔记本电脑和台式电脑共120台，购买笔记本电脑用了7.2万元，购买台式电脑用了24万元，已知笔记本电脑单价是台式电脑单价的1.5倍，那么笔记本电脑和台式电脑的单价各是多少？

查看试题解析
21. 如图， $△ A B C$ 为等边三角形，点 $D$ ， $E$ 分别在边 $B C$ ， $A C$ 上，且 $A E = C D$ ， $A D$ 与 $B E$ 相交于点 $F$ ．

求：

(1)、 $∠ B F D$ 的度数；

(2)、过点 $B$ 作 $B H ⊥ A D$ 于点 $H$ ，若 $E F = 3$ ， $F H = 6$ ，求出 $A D$ 的长度．

查看试题解析
22. 如图， $△ A B C$ 中， $D$ 为 $B C$ 上一点， $∠ C = ∠ B A D$ ， $△ A B C$ 的角平分线 $B E$ 交 $A D$ 于点 $F$ .

(1)、求证： $∠ A E F = ∠ A F E$ ；

(2)、 $G$ 为 $B C$ 上一点，当 $F E$ 平分 $∠ A F G$ 且 $∠ C = 30 °$ 时，求 $∠ C G F$ 的度数.

查看试题解析
23. 已知：如图，点 $A$ ， $B$ 在 $∠ M O N$ 的边 $O M$ ， $O N$ 上， $O A$ 的垂直平分线 $C P$ 与 $O B$ 的垂直平分线 $D P$ 相交于点 $P$ ，连接 $P A$ ， $P O$ ， $P B$ ， $A B$ ．

(1)、求证：① $P A = P B$ ；② $∠ A P B = 2 ∠ C P D$ ；

(2)、探究： $∠ M O N$ 满足什么条件时， $△ P A B$ 是等边三角形，并说明理由；

(3)、若 $O A = O B$ ，请在备用图中画出符合条件的图形，并探究 $∠ C P O$ 与 $∠ A P B$ 之间的数量关系，并说明理由．

查看试题解析