安徽省安庆市怀宁县2020-2021学年八年级上学期数学期末试卷
试卷更新日期：2021-09-27 类型：期末考试
一、单选题
-
1. 在平面直角坐标系内，下列的点位于第四象限的是（ ）A、（﹣2，1） B、（﹣2，﹣1） C、（2，﹣1） D、（0，﹣1）2. 自新冠肺炎疫情发生以来，全国人民共同抗疫．下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（ ）A、
B、
C、
D、
3. 若点（2，y1）和（﹣2，y2）都在直线y＝﹣x+3上，则y1与y2的大小关系是（ ）A、y1 y2 B、y1＝y2 C、y1 y2 D、无法确定4. 为了估计池塘A，B两点之间的距离，小明在池塘的一侧选取一点C，测得AC＝3m，BC＝6m，则A，B两点之间的距离可能是（ ）A、11m B、9m C、7m D、3m5. 下列命题中是假命题的是（ ）A、全等三角形的对应角相等 B、三角形的外角大于任何一个内角 C、等边对等角 D、角平分线上的点到角两边的距离相等6. 如图，∠ABD＝∠CBD，现添加以下条件不能判定△ABD≌△CBD的是（ ）
A、∠A＝∠C B、∠BDA＝∠BDC C、AB＝CB D、AD＝CD7. 如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB于点D．若∠A＝30°，AE＝10，则CE的长为（ ）
A、5 B、4 C、3 D、28. 若实数a，b满足ab＜0，且a＜b，则函数y＝ax＋b的图像可能是（ ）A、
B、
C、
D、
9. 如图，过点A1（2，0）作x轴的垂线，交直线y＝2x于点B1；点A2与点O关于直线A1B1对称；过点A2（4，0）作x轴的垂线，交直线y＝2x于点B2；点A3与点O关于直线A2B2对称；过点A3作x轴的垂线，交直线y＝2x于点B3；…，按此规律作下去，则点B2021的坐标为（ ）
A、（22021 ， 22020） B、（22021 ， 22022） C、（22022 ， 22021） D、（22020 ， 22021）10. 2020年12月22日8时38分，G8311次动车组列车从合肥南站始发，驶向沿江千年古城、“黄梅戏”故乡安庆．这标志着京港高铁合肥至安庆段正式开通运营．运行期间，一列动车匀速从合肥开往安庆，一列普通列车匀速从安庆开往合肥，两车同时出发，设普通列车行驶的时间为x（h），两车之间的距离y（km），图中的折线表示y与x之间的函数关系，下列说法正确的有（ ）①合肥、安庆两地相距176km，两车出发后0.5h相遇；
②普通列车到达终点站共需2h；
③普通列车的平均速度为88km/h；
④动车的平均速度为250km/h．
A、1个 B、2个 C、3个 D、4个二、填空题
-
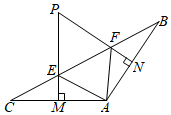
11. 函数 中，自变量 的取值范围为 ．12. 已知点A（3，0）和B（1，3），如果直线y＝kx+1与线段AB有公共点，那么k的取值范围是 ．13. 已知一次函数y＝kx+3（k 0）的图象与两坐标轴围成的三角形的面积为3，则一次函数的表达式为 ．14. 已知C，D两点在线段AB的垂直平分线上，且∠ACB＝50°，∠ADB＝86°，则∠CAD的度数是 ．15. 如图，在△ABC中，∠BAC＝124°，分别作AC，AB两边的垂直平分线PM，PN，垂足分别是点M，N．以下说法：①∠P＝56°；②∠EAF＝68°；③PE＝PF；④点P到点B和点C的距离相等．正确的是（填序号）．
三、解答题
-
16. 如图，在平面直角坐标系中，已知点A（﹣2，﹣2），B（﹣4，﹣1），C（﹣4，﹣4）．
(1)、画出△ABC向右平移5个单位，再向上平移4个单位得到的△A1B1C1 ， 其中点C1的坐标为 ▲ ；(2)、在x轴上画出点P，使PA+PB最小，此时点P的坐标为 ▲ ．17. 如图，在△ABC中，∠BAC＝62°，∠B＝78°，AC的垂直平分线交BC于点D．
(1)、求∠BAD的度数；(2)、若AB＝8，BC＝11，求△ABD的周长．18. 如图，已知：AD＝AB，AE＝AC，AD⊥AB，AE⊥AC．猜想线段CD与BE之间的数量关系与位置关系，并证明你的猜想．
19. 定义：关于x的一次函数y＝ax+b与y＝bx+a（ab≠0）叫做一对交换函数，例如：一次函数y＝3x+4与y＝4x+3就是一对交换函数．(1)、一次函数y＝2x﹣b的交换函数是；(2)、当b≠﹣2时，（1）中两个函数图象交点的横坐标是；(3)、若（1）中两个函数图象与y轴围成的三角形的面积为4，求b的值．20. 如图，在△ABC中，AB＝BC，∠B＝90°，AD是∠BAC的平分线，CE⊥AD于点E．求证：AD＝2CE．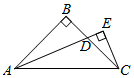
21. 2020年以来，新冠肺炎疫情肆虐全球，感染人数不断攀升，口罩瞬间成为需求最为迫切的防疫物资．为了缓解供需矛盾，在中央的号召下，许多企业纷纷跨界转行生产口罩．我县某工厂接到订单任务，要求用7天时间生产A、B两种型号的口罩，共不少于5.8万只，其中A型口罩只数不少于B型口罩．该厂的生产能力是：每天只能生产一种口罩，如果2天生产A型口罩，3天生产B型口罩，一共可以生产4.6万只；如果3天生产A型口罩，2天生产B型口罩，一共可以生产4.4万只，并且生产一只A型口罩可获利0.5元，生产一只B型口罩可获利0.3元．(1)、试求出该厂的生产能力，即每天能生产A型口罩或B型口罩多少万只？(2)、在完成订单任务的前提下，应怎样安排生产A型口罩和B型口罩的天数，才能使获得的总利润最大，最大利润是多少万元？22. 数学模型学习与应用：(1)、学习：如图1，∠BAD＝90°，AB＝AD，BC⊥AC于点C，DE⊥AC于点E．由∠1+∠2＝∠2+∠D＝90°，得∠1＝∠D；又∠ACB＝∠AED＝90°，可以通过推理得到△ABC≌△DAE，进而得到AC＝ ， BC＝ ． 我们把这个数学模型称为“一线三等角”模型．
(2)、应用：如图2，在△ABC中，AB＝AC，点D，A，E都在直线l上，并且∠BAD＝∠AEC＝∠BAC＝α．若DE＝a，BD＝b，求CE的长度（用含a，b的代数式表示）；
(3)、拓展：如图3，在（2）的条件下，若α＝120°，且△ACF是等边三角形，试判断△DEF的形状，并说明理由．