山西省运城市2021届高三上学期理数期中考试试卷

试卷更新日期：2021-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 已知命题 $p ： \forall x \in R$ ， $x - 1 > 0$ ，则 $\neg p$ （）

A、 $\exists x \in R$ ， $x - 1 \leq 0$ B、 $\exists x \in R$ ， $x - 1 > 0$ C、 $\forall x \in R$ ， $x - 1 \leq 0$ D、 $\forall x \in R$ ，x-1≥0

查看试题解析
2. 设集合 $A = {- 1 ， 0 ， 1 ， 2}$ ， $B = {x | y = \sqrt{x^{2} - 4}}$ ，则 $A \cap (∁_{R} B)$ 等于（）

A、{1} B、{0} C、 ${- 1 ， 0}$ D、 ${- 1 ， 0 ， 1}$

查看试题解析
3. 设函数 $f (x) = {\begin{array}{l} \log_{2} (1 - x) ， x < 0 \\ 4^{x} ， x \geq 0 \end{array}$ ，则 $f (- 1) + f (\log_{2} 3) =$ （）

A、9 B、10 C、11 D、12

查看试题解析
4. 设 $\vec{a}$ ， $\vec{b}$ 均为单位向量且夹角为 $θ$ ，则“ $| \vec{a} + \vec{b} | > | \vec{a} - \vec{b} |$ ”是“ $θ$ 为锐角”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 如图， $△ A B C$ 中，E是AB的中点，点F满足 $\vec{B F} = 2 \vec{F C}$ ，则 $\vec{E F} =$ （）

A、 $- \frac{1}{6} \vec{A B} + \frac{2}{3} \vec{A C}$ B、 $\frac{1}{6} \vec{A B} + \frac{2}{3} \vec{A C}$ C、 $- \frac{1}{6} \vec{A B} + \frac{1}{3} \vec{A C}$ D、 $\frac{1}{2} \vec{A B} + \frac{1}{3} \vec{A C}$

查看试题解析
6. 已知 $2 a = \log_{\frac{1}{3}} a$ ， $b = x^{2} - x + \frac{3}{4}$ ， $c = \ln \frac{\sqrt{2}}{2}$ ，则a，b，c的大小关系是（）

A、 $a > b > c$ B、 $a > c > b$ C、 $b > c > a$ D、 $b > a > c$

查看试题解析
7. 函数 $f (x) = \frac{3 \sin x}{2^{| x |}} + x \cos x$ 在 $[- 2 π ， 2 π]$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
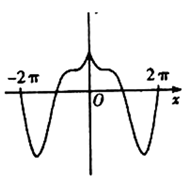8. 若 $S_{n} = \cos \frac{π}{5} + \cos \frac{2 π}{5} + \dots + \cos \frac{(n - 1) π}{5} + \cos \frac{n π}{5} (n \in N^{*})$ ，则 $S_{1}$ 、 $S_{2}$ 、 $\dots$ 、 $S_{2020}$ 中值为 $0$ 的共有（）

A、202个 B、404个 C、606个 D、808个

查看试题解析
9. 将函数 $f (x) = \sin (2 x + φ)$ 的图象向左平移 $\frac{π}{4}$ 个单位后得到函数 $g (x)$ 的图象， $g (x)$ 的图象在 $x = \frac{π}{6}$ 处切线垂直于y轴，且 $g (π) + g (\frac{π}{4}) > 0$ ，则当 $φ$ 取最小正数时，不等式 $g (x) \geq \frac{1}{2}$ 的解集是（）

A、 $[k π - \frac{π}{3} ， k π + \frac{π}{6}] (k \in Z)$ B、 $[k π ， k π + \frac{π}{3}] (k \in Z)$ C、 $[k π - π ， k π - \frac{2}{3} π] (k \in Z)$ D、 $[k π - \frac{π}{2} ， k π] (k \in Z)$

查看试题解析
10. 已知函数 $f (x) = x^{5} + 3 x^{3} + x + 2$ ，若 $f (a) + f (a - 2) > 4$ ，则实数a的取值范围是（）

A、 $(- \infty ， 1)$ B、 $(- \infty ， 2)$ C、 $(1 ， + \infty)$ D、 $(2 ， + \infty)$

查看试题解析
11. 若数列 ${a_{n}}$ 的通项公式为 $a_{n} = 2^{n} - 1$ ，在一个 $n$ 行 $n$ 列的数表中，第 $i$ 行第 $j$ 列的元素为 $c_{i j} = a_{i} \cdot a_{j} + a_{i} + a_{j} (i = 1 ， 2 ， \cdot \cdot \cdot ， n ， j = 1 ， 2 ， \cdot \cdot \cdot ， n)$ ，则满足 $c_{11} + c_{22} + \cdot \cdot \cdot + c_{n n} < 2021$ 的 $n$ 的最大值是（）

A、4 B、5 C、6 D、7

查看试题解析
12. 已知函数 $f (x) = \ln a x - x (a > 0)$ 有两个零点 $x_{1}$ ， $x_{2}$ ，且 $2 x_{1} < x_{2}$ ，则a的取值范围是（）

A、 $(\frac{2}{\ln 2} ， + \infty)$ B、 $(0 ， \frac{2}{\ln 2})$ C、 $(\frac{2 \sqrt{3}}{\ln 3} ， + \infty)$ D、 $(0 ， \frac{2 \sqrt{3}}{\ln 3})$

查看试题解析

二、填空题

13. 已知 $\tan α = 2$ ，则 $\cos 2 α =$ ．

查看试题解析
14. 我国古代著名的数学专著《九章算术》里有一段叙述：今有良马和驽马发长安至齐，良马初日行一百零三里，日增十三里；驽马初日行九十七里，日减半里；良马先至齐，复还迎驽马，九日后二马相逢，则齐去长安里．

查看试题解析
15. 当 $x < 0$ 时，不等式 $x (x - k e^{x}) \geq \frac{2}{3} k e^{x}$ 恒成立，则实数k的取值范围是．

查看试题解析
16. 已知 $| \vec{a} | = 1$ ，向量 $\vec{b}$ 满足 $| \vec{b} - \vec{a} | = \vec{b} \cdot \vec{a}$ ，当 $\vec{a}$ ， $\vec{b}$ 夹角最大时， $| \vec{b} | =$ ．

查看试题解析

三、解答题

17. 已知命题p：方程 $x^{2} - a | x | + 1 = 0$ 有解；命题q：函数 $f (x) = x^{3} + 3 x^{2}$ 在区间 $[a - 1 ， a]$ 上单调递减.若命题 $p \lor q$ 为真， $p \land q$ 为假，求实数a的取值范围.

查看试题解析
18. 已知向量 $\vec{m} = (\cos x ， \sin x)$ ， $\vec{n} = (\cos x ， \sqrt{3} \cos x)$ ，设函数 $f (x) = \vec{m} \cdot \vec{n} - \frac{1}{2}$ ， $x \in [0 ， \frac{π}{3}]$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、若方程 $f (x) = \frac{2}{3}$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ，求 $\cos (x_{1} + x_{2})$ ， $\cos (x_{1} - x_{2})$ 的值．

查看试题解析
19. 已知正项数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，满足 $a_{n} = \sqrt{S_{n}} + \sqrt{S_{n - 1}}$ （ $n \geq 2$ ， $n \in N^{*}$ ）， $a_{1} = 1$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \cos n π \cdot \frac{n}{a_{n} a_{n + 1}}$ ，求数列 ${b_{n}}$ 的前 $2 n$ 项和 $T_{2 n}$ 的表达式.

查看试题解析
20. 某高档小区有一个池塘，其形状为直角 $△ A B C$ ， $∠ C = 90 °$ ， $A B = 2$ 百米， $B C = 1$ 百米，现准备养一批观赏鱼供小区居民观赏．

(1)、若在 $△ A B C$ 内部取一点P，建造APC连廊供居民观赏，如图①，使得点P是等腰三角形PBC的顶点，且 $∠ C P B = \frac{2 π}{3}$ ，求连廊 $A P + P C$ 的长；

(2)、若分别在AB，BC，CA上取点D，E，F，建造 $△ D E F$ 连廊供居民观赏，如图②，使得 $△ D E F$ 为正三角形，求 $△ D E F$ 连廊长的最小值．

查看试题解析
21. 设函数 $f (x) = x \ln x$ ．

(1)、设 $g (x) = \frac{f^{'} (x)}{x}$ ，求 $g (x)$ 的极值点；

(2)、若 $x_{2} > x_{1} > 0$ 时，总有 $\frac{m}{2} (x_{2}^{2} - x_{1}^{2}) > f (x_{2}) - f (x_{1})$ 恒成立，求实数m的取值范围．

查看试题解析
22. 已知函数 $f (x) = e^{x} \sin x$ （ $e$ 是自然对数的底数）．

(1)、设 $s (x) = e^{x} - f (x)$ ， $x \in [0 ， \frac{π}{2}]$ ，求证： $0 \leq s (x) \leq 1$ ；

(2)、设 $g (x) = f (x) - a x$ ，若 $0 < a < 3$ ，试讨论 $g (x)$ 在 $(0 ， π)$ 上的零点个数．（参考数据 $e^{\frac{π}{2}} \approx 4.8$ ）

查看试题解析