四川省遂宁市安居区2020-2021学年高二上学期理数期中考试试卷
试卷更新日期:2021-09-27 类型:期中考试
一、单选题
-
1. 直线 的倾斜角为( )A、0 B、 C、 D、2. 两条异面直线所成的角的范围是( )A、 B、 C、 D、3. 如图,直线 , , 的斜率分别为 , , ,则( )
 A、 B、 C、 D、4. 下列关于直线 ,点 与平面 的关系推理错误的是( )A、 B、 C、 D、5. 点 关于直线 对称的点 ´的坐标是( )A、 B、 C、 D、6. 与直线 关于 轴对称的直线的方程为( )A、 B、 C、 D、7. 如图所示, 垂直于以 为直径的圆 所在的平面, 为圆上异于 的任一点,则下列关系中不正确的是( )
A、 B、 C、 D、4. 下列关于直线 ,点 与平面 的关系推理错误的是( )A、 B、 C、 D、5. 点 关于直线 对称的点 ´的坐标是( )A、 B、 C、 D、6. 与直线 关于 轴对称的直线的方程为( )A、 B、 C、 D、7. 如图所示, 垂直于以 为直径的圆 所在的平面, 为圆上异于 的任一点,则下列关系中不正确的是( ) A、 B、 平面 C、 D、8. 已知实数 满足 ,则 的最小值是 )A、2 B、1 C、 D、9. 已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的表面积为( )A、 B、2π C、π D、10. 已知 是三条不同的直线, 是三个不同的平面,有下列命题:
A、 B、 平面 C、 D、8. 已知实数 满足 ,则 的最小值是 )A、2 B、1 C、 D、9. 已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的表面积为( )A、 B、2π C、π D、10. 已知 是三条不同的直线, 是三个不同的平面,有下列命题:① ②若 则 ③ 则 ④直线 ,直线 ,那么 ⑤若 ,则 ⑥若 ,则 ,
其中所有正确命题数( )
A、1 B、2 C、3 D、411. 设点 ,若直线 与线段 有交点,则 的取值范围是( )A、 B、 C、 D、12. 函数 为定义在 上的减函数,函数 的图像关于点(1,0)对称,若 满足不等式 ,则当 时,求x+2y的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 点 到直线 的距离为14. 已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 cm3 .
 15. 如图所示,正方体 的棱长为 是底面 的中心,则 到平面 的距离为 .
15. 如图所示,正方体 的棱长为 是底面 的中心,则 到平面 的距离为 . 16. 点P在正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:
16. 点P在正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:
①直线AD与直线B1P为异面直线;②A1P 面ACD1;③三棱锥A-D1PC的体积为定值;④面PDB1⊥面ACD1.⑤直线 与平面 所成角的大小不变;
其中所有正确命题的序号是.
三、解答题
-
17. 已知直线过点 和 两点(1)、求出该直线的直线方程(用点斜式表示)(2)、将(1)中直线方程化成斜截式,一般式以及截距式且写出直线在x轴和y轴上的截距.18. 如图,在直三棱柱 中, ,点 是 的中点.
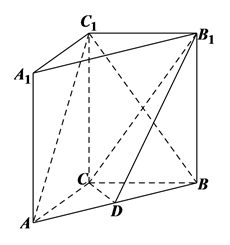
求证:
(1)、 ;(2)、 平面 .19. 已知直线 .(1)、若 ,求实数 的值;(2)、当 时,求直线 与 之间的距离.

