北师版数学九年级上册《第六章 反比例函数》单元检测B卷
试卷更新日期:2021-09-25 类型:单元试卷
一、单选题
-
1. 如图,已知直线y=k1x(k1≠0)与反比例函数y= (k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( )
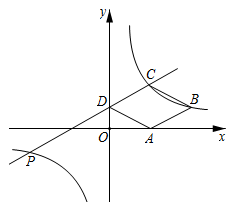
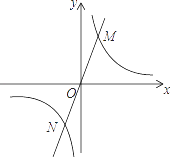 A、(﹣1,﹣2) B、(﹣1,2) C、(1,﹣2) D、(﹣2,﹣1)2. 如图,反比例函数 的图象经过点 ,过A作 轴于点B,连 ,直线 ,交x轴于点C,交y轴于点D,若点B关于直线 的对称点 恰好落在该反比例函数图象上,则D点纵坐标为( )
A、(﹣1,﹣2) B、(﹣1,2) C、(1,﹣2) D、(﹣2,﹣1)2. 如图,反比例函数 的图象经过点 ,过A作 轴于点B,连 ,直线 ,交x轴于点C,交y轴于点D,若点B关于直线 的对称点 恰好落在该反比例函数图象上,则D点纵坐标为( )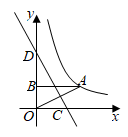 A、 B、 C、 D、3. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、4. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )
A、 B、 C、 D、3. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、4. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )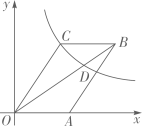 A、 B、 C、 D、5. 已知点 在反比例函数 的图象上.若 ,则( )A、 B、 C、 D、6. 如图.在平面直角坐标系中,△AOB的面积为 ,BA垂直x轴于点A,OB与双曲线y= 相交于点C,且BC∶OC=1∶2,则k的值为( )
A、 B、 C、 D、5. 已知点 在反比例函数 的图象上.若 ,则( )A、 B、 C、 D、6. 如图.在平面直角坐标系中,△AOB的面积为 ,BA垂直x轴于点A,OB与双曲线y= 相交于点C,且BC∶OC=1∶2,则k的值为( )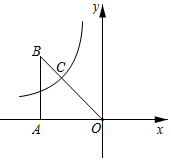 A、﹣3 B、﹣ C、3 D、7. 如图, 交双曲线 于点A , 且 ,若矩形 的面积是8,且 轴,则k的值是( )
A、﹣3 B、﹣ C、3 D、7. 如图, 交双曲线 于点A , 且 ,若矩形 的面积是8,且 轴,则k的值是( )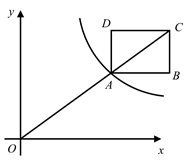 A、18 B、50 C、12 D、8. 如图,O是坐标原点,点B在x轴上,在 OAB中,AO=AB=5,OB=6,点A在反比例函数y= (k≠0)图象上,则k的值( )
A、18 B、50 C、12 D、8. 如图,O是坐标原点,点B在x轴上,在 OAB中,AO=AB=5,OB=6,点A在反比例函数y= (k≠0)图象上,则k的值( ) A、﹣12 B、﹣15 C、﹣20 D、﹣309. 已知:如图,直线 与双曲线 在第一象限交于点 ,与x轴、y轴分别交于A,B两点,则下列结论错误的是( )
A、﹣12 B、﹣15 C、﹣20 D、﹣309. 已知:如图,直线 与双曲线 在第一象限交于点 ,与x轴、y轴分别交于A,B两点,则下列结论错误的是( )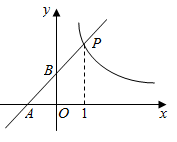 A、 B、 是等腰直角三角形 C、 D、当 时,10. 如图,点A在曲线到 上,点B在双曲线 上, 轴,点C是x轴上一点,连接 、 ,若 的面积是6,则k的值( )
A、 B、 是等腰直角三角形 C、 D、当 时,10. 如图,点A在曲线到 上,点B在双曲线 上, 轴,点C是x轴上一点,连接 、 ,若 的面积是6,则k的值( )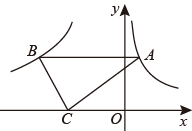 A、-6 B、-8 C、-10 D、-1211. 在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 ,则点A的坐标为( )A、 B、 C、 D、12. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )
A、-6 B、-8 C、-10 D、-1211. 在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 ,则点A的坐标为( )A、 B、 C、 D、12. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )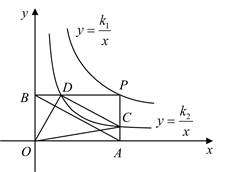 A、①② B、①③ C、②③ D、①
A、①② B、①③ C、②③ D、①二、填空题
-
13. 若反比例函数 的图象过点 ,则k的值等于.14. 如图,点 分别在函数 的图象上,点 在 轴上.若四边形 为正方形,点 在第一象限,则 的坐标是.
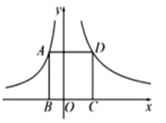 15. 如图,若反比例函数 的图象经过等边三角形POQ的顶点P,则△POQ的边长为.
15. 如图,若反比例函数 的图象经过等边三角形POQ的顶点P,则△POQ的边长为.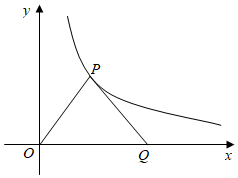 16. 如图, 、 两点在反比例函数 ( )的图象上, 的延长线交 轴于点 ,且 ,则 的面积是.
16. 如图, 、 两点在反比例函数 ( )的图象上, 的延长线交 轴于点 ,且 ,则 的面积是.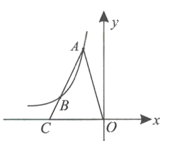 17. 如图,平行于y轴的直线与函数y1 (x>0)和y2 (x>0)的图象分别交于A、B两点,OA交双曲线y2 于点C,连接CD,若 OCD的面积为2,则k=.
17. 如图,平行于y轴的直线与函数y1 (x>0)和y2 (x>0)的图象分别交于A、B两点,OA交双曲线y2 于点C,连接CD,若 OCD的面积为2,则k=.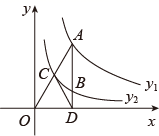 18. 如图,矩形 的顶点 在反比例函数 的图象上,矩形 的面积为3,则 ;
18. 如图,矩形 的顶点 在反比例函数 的图象上,矩形 的面积为3,则 ;
三、解答题
-
19. 如图,点A(﹣2,y1)、B(﹣6,y2)在反比例函数y= (k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC与BD相交于点E.
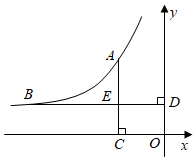 (1)、根据图象直接写出y1、y2的大小关系,并通过计算加以验证;(2)、结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 ▲ (只填序号).20. 如图,已知直线y=kx+b(k≠0)与双曲线y= 相较于A(m,3)、B(3,n)两点.
(1)、根据图象直接写出y1、y2的大小关系,并通过计算加以验证;(2)、结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 ▲ (只填序号).20. 如图,已知直线y=kx+b(k≠0)与双曲线y= 相较于A(m,3)、B(3,n)两点. (1)、求直线AB的解析式;(2)、连结AO并延长交双曲线于点C,连结BC交x轴于点D,连结AD,求△ABD的面积.21. 如图,一次函数y=x+2的图象与反比例函数 的图象相交,其中一个交点的横坐标是1.
(1)、求直线AB的解析式;(2)、连结AO并延长交双曲线于点C,连结BC交x轴于点D,连结AD,求△ABD的面积.21. 如图,一次函数y=x+2的图象与反比例函数 的图象相交,其中一个交点的横坐标是1.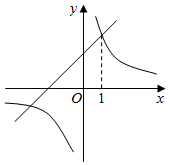 (1)、求k的值;(2)、若将一次函数y=x+2的图象向下平移4个单位长度,平移后所得到的图象与反比例函数 的图象相交于A,B两点,求此时线段AB的长.22. 如图,一次函数y=ax+b的图象与反比例函数 的图象交于点A、B,与x轴交于点 ,若OC=AC,且 =10
(1)、求k的值;(2)、若将一次函数y=x+2的图象向下平移4个单位长度,平移后所得到的图象与反比例函数 的图象相交于A,B两点,求此时线段AB的长.22. 如图,一次函数y=ax+b的图象与反比例函数 的图象交于点A、B,与x轴交于点 ,若OC=AC,且 =10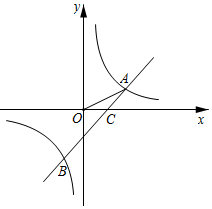 (1)、求反比例函数与一次函数的表达式;(2)、请直接写出不等式ax+b> 的解集.23. 小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:(1)、绘制函数图象
(1)、求反比例函数与一次函数的表达式;(2)、请直接写出不等式ax+b> 的解集.23. 小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:(1)、绘制函数图象①列表:下表是 与 的几组对应值,其中 ▲ ;
…
-4
-3
-2
0
1
2
…
…
-1
=2
-3
3
2
…
②描点:根据表中的数值描点 ,请补充描出点 ;
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.
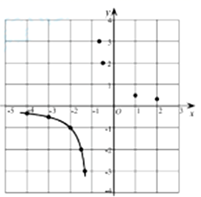 (2)、探究函数性质
(2)、探究函数性质判断下列说法是否正确。
①函数值 随 的增大而减小:
②函数图象关于原点对称:
③函数图象与直线 没有交点.