浙江省温州地区2021-2022学年九年级上学期数学返校考试试卷
试卷更新日期:2021-09-24 类型:开学考试
一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选多选、错选均不给分
-
1. 在0, ,-3,2这四个数中,最大的数是( )A、0 B、 C、-3 D、22. 太阳半径约696000000米,其中数据696000000用科学记数法表示为( )A、0.696×109 B、6.96×109 C、6.96×108 D、696×1063. 估计的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间4. 若分式的值为0,则x的取值应满足( )A、4 B、-4 C、0 D、x≠05. 下列函数中,属于二次函数的是( )A、y=x﹣3 B、y=x2﹣(x+1)2 C、y=x(x﹣1)﹣1 D、6. 下面计算正确的是( )A、 B、 C、 D、7. 用配方法解方程时,配方变形结果正确的是( )A、(x+3)2=8 B、(x-3)2=8 C、(x+3)2=10 D、(x-3)2=108. 在平面直角坐标系中,将抛物线y=x2-4先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )A、y=(x+2)2+2 B、y=(x-2)2-2 C、y=(x-2)2+2 D、y=(x+2)2-29. 如图,正方形ABCD的面积为12,△ABE是等边三角形且点E在正方形内,点P在对角线AC上,连结PD,PE,则PD+PE的最小值为( )
 A、12 B、6 C、 D、10. 如图,将图甲表示的正方形纸片剪成四块,恰好拼成图乙表示的矩形.若x=1,则y等于( )
A、12 B、6 C、 D、10. 如图,将图甲表示的正方形纸片剪成四块,恰好拼成图乙表示的矩形.若x=1,则y等于( )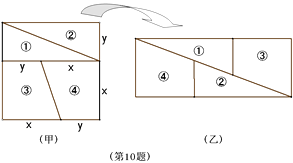 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6小题,每小题5分,共30分):
-
11. 分解因式: = .12. 若二次根式
 有意义,则x的取值范围是 . 13. 若关于x的方程x2-mx+3=0有实数根,则m的值可以为 . (任意给出一个符合条件的值即可)14. 如图,∠1,∠2,∠3是五边形ABCDE的3个外角,若∠A+∠B=240°,则∠1+∠2+∠3= .
有意义,则x的取值范围是 . 13. 若关于x的方程x2-mx+3=0有实数根,则m的值可以为 . (任意给出一个符合条件的值即可)14. 如图,∠1,∠2,∠3是五边形ABCDE的3个外角,若∠A+∠B=240°,则∠1+∠2+∠3= . 15. 如图,在第一象限内,点A,B在反比例函数 的图像上,点C在反比例函数 的图像上,AC∥ 轴,BC∥ 轴,若BC=3,AC=4,则 =
15. 如图,在第一象限内,点A,B在反比例函数 的图像上,点C在反比例函数 的图像上,AC∥ 轴,BC∥ 轴,若BC=3,AC=4,则 = 16. 如图,在平行四边形ABCD中,点E是边AD上一点,CD=CE,连结BE,将△DCE 沿CE翻折,点D的对应点F恰好落在BE上,连结CF,若∠A=105°,△ABE的面积为 ,则ED= cm.
16. 如图,在平行四边形ABCD中,点E是边AD上一点,CD=CE,连结BE,将△DCE 沿CE翻折,点D的对应点F恰好落在BE上,连结CF,若∠A=105°,△ABE的面积为 ,则ED= cm.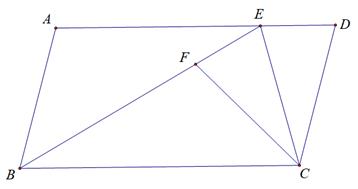
三、解答题(本题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)
-
17.(1)、计算:(2)、化简:18.(1)、解方程:(2)、解不等式组:19. 如图,在▱ABCD中,对角线AC,BD相交于点O,BE⊥AC于点E,CF⊥BD于点F,BE CF.
 (1)、求证:▱ABCD是矩形.(2)、若OD=13,CF=12,求BF的长.20. 如图5×5方格中,小正方形边长为1个单位长度,每个小正方形的顶点叫做格点.请按下列要求画出一个符合题意的四边形,且顶点在格点上,
(1)、求证:▱ABCD是矩形.(2)、若OD=13,CF=12,求BF的长.20. 如图5×5方格中,小正方形边长为1个单位长度,每个小正方形的顶点叫做格点.请按下列要求画出一个符合题意的四边形,且顶点在格点上,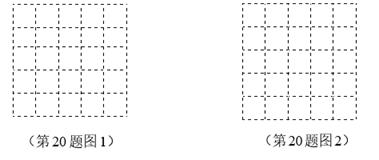 (1)、在图1中画:是中心对称图形,但不是轴对称图形,且面积为8;(2)、在图2中画:既是中心对称图形又是轴对称图形,且各边长都是无理数,面积为10.21. 为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:
(1)、在图1中画:是中心对称图形,但不是轴对称图形,且面积为8;(2)、在图2中画:既是中心对称图形又是轴对称图形,且各边长都是无理数,面积为10.21. 为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图所示的两个统计图(部分未完成).请根据图中信息,回答下列问题: (1)、校团委随机调查了 名学生,并请你补全条形统计图 ;(2)、被调查的部分学生一周零花钱的平均数是元,中位数是 元.(3)、“50元”所在扇形的圆心角的度数为 .(4)、为捐助贫困山区希望小学,全校1000名学生每人自发地捐出一周零花钱,请估算全校学生共捐款多少元?22. 如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).
(1)、校团委随机调查了 名学生,并请你补全条形统计图 ;(2)、被调查的部分学生一周零花钱的平均数是元,中位数是 元.(3)、“50元”所在扇形的圆心角的度数为 .(4)、为捐助贫困山区希望小学,全校1000名学生每人自发地捐出一周零花钱,请估算全校学生共捐款多少元?22. 如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).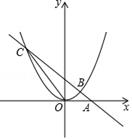 (1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.23. 瑞安市高楼绿道有二人座,三人座,四人座三种规格的共享单车供游客租赁,其收费标准如下表:
(1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.23. 瑞安市高楼绿道有二人座,三人座,四人座三种规格的共享单车供游客租赁,其收费标准如下表:车型 二人座 三人座 四人座 价格(元/小时) 20 40 60 某单位组织员工到该景点春游,共租赁n辆这三种共享单车,且三人座共享单车是二人座共享单车数量的2倍。
(1)、当n=20时,①若该单位有60人,租赁的每辆车都坐满人,则租赁了多少辆三人座的共享单车?
②请设计一个租金金额最少的方案,并求出租金金额;
(2)、若该单位主管打算用于租这三种共享单车的总资金为2080元,则最多能租多少辆共享单车供员工使用?24. 如图,在直角坐标系中直线AB与x、y轴分别交于点A、B两点,已知B(0,4),∠BAO=30°,P,Q分别是线段OB,AB上的两个动点,点P从O出发以每秒3个单位长度的速度向终点B运动,点Q从B出发以每秒8个单位长度的速度向终点A运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为t(秒)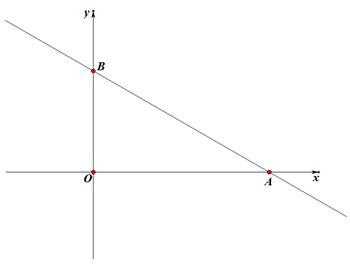
 (1)、求点A的坐标和线段AB的长;(2)、当t为何值时,△BPQ的面积为2 ;(3)、若C为OA的中点,连结QC,QP,以QC,QP为邻边作平行四边形PQCD,
(1)、求点A的坐标和线段AB的长;(2)、当t为何值时,△BPQ的面积为2 ;(3)、若C为OA的中点,连结QC,QP,以QC,QP为邻边作平行四边形PQCD,
①t为何值时,点D恰好落在坐标轴上;
②是否存在这样的 ,使x轴将平行四边形PQCD的面积分成1:3的两部分,若存在,请直接写出 的值。