浙江省金华市婺城区2021年数学初中毕业升学考试模拟测试试卷（三）

试卷更新日期：2021-09-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 2021的绝对值是（）

A、 $\frac{1}{2021}$ B、﹣ $\frac{1}{2021}$ C、2021 D、﹣2021

查看试题解析
2. 习近平总书记提出了未来五年“精准扶贫”的战略构想，意味着每年要减贫约11700000人，将数据11700000用科学记数法表示为（）

A、1.17×10⁷ B、11.7×10⁶ C、0.117×10⁷ D、1.17×10⁸

查看试题解析
3. 一种面粉的质量标识为“ $25 \pm 0.25$ ”千克，则下列面粉中合格的有（）

A、25.30 B、2525.51.51 C、 $24.80$ D、24.70

查看试题解析
4. 同学们，你们都知道吸烟有害健康，却不知被动吸烟也有害健康，为了你我他的健康，请不要吸烟.如果小明同学要了解人们被动吸烟的情况，则他选择最合适的调查方式是（）

A、在学校里随机调查 B、在社会上随机调查 C、普查 D、抽样

查看试题解析
5. 视力表用来测量一个人的视力.如图是视力表的一部分，其中开口向下的两个“E”之间的变换是（）

A、平移 B、旋转 C、轴对称 D、位似

查看试题解析
6. 下列手机手势解锁图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 若∠A，∠B都是锐角，且tanA=1，sinB= $\frac{\sqrt{2}}{2}$ ，则△ABC不可能是（ )

A、等腰三角形 B、等腰直角三角形 C、锐角三角形 D、直角三角形

查看试题解析
8. 如图，在△ABC中，∠C＝90°，∠B＝15°，AC＝1，分别以点A，B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧交于点M，N，作直线MN交BC于点D，连接AD，则AD的长为（）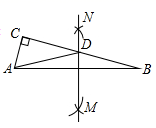

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、2 D、5

查看试题解析
9. 七巧板是我国祖先的一项卓越创造，下列四幅图是爱思考的小红同学用如图所示的七巧板拼成的，则这四个图形的周长从大到小排列正确的是（）

A、乙＞丙＞甲＞丁 B、乙＞甲＞丙＞丁 C、丙＞乙＞甲＞丁 D、丙＞乙＞丁＞甲

查看试题解析
10. 如图1，动点K从△ABC的顶点A出发，沿AB﹣BC匀速运动到点C停止，在动点K运动过程中，线段AK的长度y与运动时间x的函数关系如图2所示，其中点D为曲线部分的最低点，若△ABC的面积是10 $\sqrt{6}$ 则a＝（　　）

A、7 B、 $3 \sqrt{6}$ C、8 D、 $4 \sqrt{6}$

查看试题解析

二、填空题

11. 函数y＝ $\sqrt{1 - x}$ 中，自变量x的取值范围是．

查看试题解析
12. 因式分解： $a^{3} - 4 a =$ ．

查看试题解析
13. 不等式组 ${\begin{cases} x + 2 > 1 \\ 2 x - 1 \leq 8 - x \end{cases}$ 的最大整数解是．

查看试题解析
14. 把两个同样大小含 $30^{\circ}$ 角的三角尺按如图所示的方式放置， $∠ A C B = ∠ D B E = 30^{\circ}$ ，其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点B，且另外三个锐角顶点C，A，E在同一直线上，若 $A B = 2$ ，则 $A E =$ .

查看试题解析
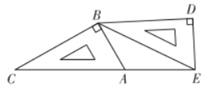15. 如图所示，在扇形OAB中，∠AOB＝90°，OA＝2，长为2的线段CD的两个端点分别在线段OA、OB上滑动，E为CD的中点，点F在弧AB上，连接EF、BE.若AF的长是 $\frac{π}{3}$ ，当线段EF的值最小时图中阴影部分的面积是.

查看试题解析
16. 寒假在家学习网课时，小李将笔记本电脑水平放置在桌子上，显示屏OB与底板OA所在水平线的夹角为120°，此时感觉最舒适（如图1），侧面示意图为图2.使用时为了散热，他在底板下垫入散热架ACO′后，使电脑变化至AD′位置（如图3），侧面示意图为图4.已知OA＝OB＝24cm，O′C⊥OA于点C，O′C＝12cm.

(1)、∠CAO′＝；

(2)、显示屏的顶部B比原来升高了cm.

查看试题解析

三、解答题

17. 计算：2021⁰﹣ $| 1 - \sqrt{2} |$ +2sin45°+（﹣2）^﹣¹.

查看试题解析
18. 先化简 $\frac{2 a + 2}{a - 1} \div (a + 1) + \frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ，然后a在﹣1，1，2三个数中任选一个合适的数代入求值．

查看试题解析
19. 图1、图2是8×8的网格，网格中每个小正方形的边长均为1，请按要求画出下列图形，所画图形的各个顶点均在小正方形的顶点上。

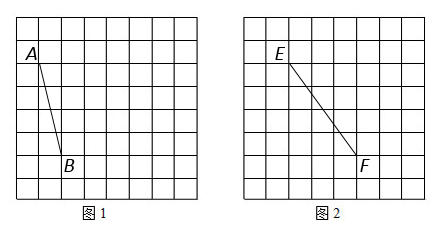(1)、在图1中画出以AB为一边的成中心对称的四边形ABCD，使其面积为12；

(2)、在图2中画出一个以EF为一边的△EFG，使其是面积为 $\frac{15}{2}$ 的轴对称图形。

查看试题解析
20. “校园安全”受到全社会的广泛关注，某校对部分学生及家长就校园安全知识的了解程度，进行了随机抽样调查，并给制成如图所示的两幅统计图，请根据统计图中的信息，解答下列问题：

(1)、参与调查的学生及家长共有人；

(2)、在扇形统计图中，“基本了解”所对应的圆心角的度数是度；在条形统计图中，“非常了解”所对应的学生人数是人；

(3)、若全校有2050名学生，请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人？

查看试题解析
21. 如图，在△ABC中，AB＝BC，D是AC中点，BE平分∠ABD交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F.

(1)、判断直线AC与⊙O的位置关系，并说明理由；

(2)、当BD＝6，AB＝10时，求BG的长.

查看试题解析
22. 某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．

(1)、求水柱所在抛物线（第一象限部分）的函数表达式；

(2)、王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

(3)、经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．

查看试题解析

23. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后，进一步研究函数

y = \frac{3}{| x |}

的图象与性质.其探究过程如下：

(1)、绘制函数图象，如图.

列表：下表是 $x$ 与 $y$ 的几组对应值，其中 $m =$ ▲ ；

$x$	…	-3	-2	-1	$- \frac{1}{3}$	$\frac{1}{3}$	1	2	3	…
$y$	…	1	$\frac{3}{2}$	3	9	9	3	$m$	1	…

描点：根据表中各组对应值 $(x ， y)$ ，在平面直角坐标系中描出了各点：

连线：用平滑的曲线顺次连接各点，画出了部分图象，请你把图象补充完整；

(2)、通过观察图象，写出该函数的两条性质：①；②；

(3)、①观察发现：若直线

y = 3

交函数

y = \frac{3}{| x |}

的图象于

A

，

B

两点，连接

O A

，过点

B

作

B C // O A

交

x

轴于

C

，则

S_{四 边 形 O A B C} =

；

②探究思考：将①中“直线 $y = 3$ ”改为“直线 $y = a (a > 0)$ ”，其他条件不变，则 $S_{四边形 O A B C} =$ ；

③类比猜想：若直线 $y = a (a > 0)$ 交函数 $y = \frac{k}{| x |} (k > 0)$ 的图象于 $A$ ， $B$ 两点，连接 $O A$ ，过点 $B$ 作 $B C // O A$ 交轴于 $C$ ，则 $S_{四边形 O A B C} =$ ；

查看试题解析

24. 在矩形ABCD中，AB＝4，点P是直线CD上（不与点C重合）的动点，连结BP，过点B作BP的垂线分别交直线AD、直线CD于点E、F，连结PE.

(1)、如图，当AD＝4，点P是CD的中点时，求tan∠EBA的值：

(2)、当AD＝2时
①若△DPE与△BPE相似，求DP的长.

②若△PEF是等腰三角形，求DE的长.

查看试题解析