浙江省杭州市余杭区2021年数学中考二模试卷
试卷更新日期:2021-09-24 类型:中考模拟
一、单选题
-
1. ﹣20+21=( )A、﹣1 B、1 C、﹣2021 D、20212. (1﹣x)2=( )A、1﹣x2 B、1+x2 C、1﹣2x+x2 D、1+2x+x23. 某冰箱冷藏室的温度是5℃,冷冻室的温度比冷藏室的温度低17℃,则冷冻室的温度是多少摄氏度?( )A、12℃ B、﹣12℃ C、22℃ D、﹣22℃4. 若sinα= ,则锐角α=( )A、30° B、45° C、50° D、60°5. 下列说法中正确的是( )A、若x>3,则x>4 B、若x>3,则x<4 C、若x>4,则x>3 D、若x>4,则x<36. 笼中有鸡兔共25只,且有60只脚,设鸡有x只,则可列方程为( )A、2x+4x=6 B、2x+2(25﹣x)=60 C、4x+4(25﹣x)=60 D、2x+4(25﹣x)=607. 篮球队5名场上队员的身高(单位:cm)分别是:188,190,192,194,195.现用一名身高为191cm的队员换下身高为195cm的队员,与换人前相比,场上队员的身高( )A、平均数变小,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变小 D、平均数变大,方差变大8. 在平面直角坐标系中,一次函数y=kx+b(k>0)的图象经过点(﹣1,0),则函数图象可能是( )A、
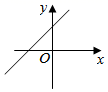 B、
B、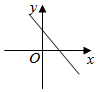 C、
C、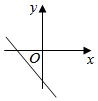 D、
D、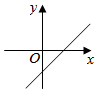 9. 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,过点C作⊙O的切线,交AB的延长线于点D.设∠A=α,∠D=β,则( )
9. 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,过点C作⊙O的切线,交AB的延长线于点D.设∠A=α,∠D=β,则( ) A、α﹣β B、α+β=90° C、2α+β=90° D、α+2β=90°10. 已知二次函数y=﹣x2+bx+c的图象与x轴交于(﹣1,0),( )A、若c>0,则对称轴在y轴右侧 B、若c>0,则对称轴在y轴左侧 C、若c<0,则对称轴在y轴右侧 D、若c<0,则对称轴在y轴左侧
A、α﹣β B、α+β=90° C、2α+β=90° D、α+2β=90°10. 已知二次函数y=﹣x2+bx+c的图象与x轴交于(﹣1,0),( )A、若c>0,则对称轴在y轴右侧 B、若c>0,则对称轴在y轴左侧 C、若c<0,则对称轴在y轴右侧 D、若c<0,则对称轴在y轴左侧二、填空题
-
11. 要使分式 有意义,x的取值应满足.12. 如图,转盘的白色扇形和黑色扇形的圆心角分别是120°和240°.让转盘自由转动1次,指针落在白色区域的概率是.
 13. 已知:如图,BC⊥AC于点C,CD⊥AB于点D,BE∥CD.若∠EBC=50°,则∠A=.
13. 已知:如图,BC⊥AC于点C,CD⊥AB于点D,BE∥CD.若∠EBC=50°,则∠A=. 14. 若方程组 的解也是方程x+ky=0的解,则k=.15. 如图,过以AB为直径的半圆O上一点C作CD⊥AB于点D.已知cos∠ACD= ,BC=6,则AC=.
14. 若方程组 的解也是方程x+ky=0的解,则k=.15. 如图,过以AB为直径的半圆O上一点C作CD⊥AB于点D.已知cos∠ACD= ,BC=6,则AC=. 16. 如图,在矩形纸片ABCD中,AB=1,点E、F分别是AB和CD的中点,H为BC上的一点,现将△ABH沿AH折叠,使点B落在直线EF上的点G.当△ADG为等腰三角形时,AD=.
16. 如图,在矩形纸片ABCD中,AB=1,点E、F分别是AB和CD的中点,H为BC上的一点,现将△ABH沿AH折叠,使点B落在直线EF上的点G.当△ADG为等腰三角形时,AD=.
三、解答题
-
17. 已知x=﹣2是关于x的方程 (1﹣2ax)=x+a的解,求a的值.18. 为了解某校九年级男生立定跳远成绩,从该校九年级450名男生中随机抽取若干名学生进行立定跳远测试,所得数据绘制成如下统计图表:
组别
跳远成绩x(m)
人数(人)
A
x<1.90
2
B
1.90≤x<2.10
m
C
2.10≤x<2.30
6
D
2.30≤x<2.50
16
E
x≥2.50
12
 (1)、求表中m的值及图中D组扇形的圆心角的度数.(2)、如果成绩达到2.30m属于优秀,那么优秀率是多少?试估算全校男生立定跳远优秀的人数.19. 如图,在△ABC中,D、E分别是AB,AC上的点,∠AED=∠B,△ABC用平分线AF交DE于点G,交BC于点F.
(1)、求表中m的值及图中D组扇形的圆心角的度数.(2)、如果成绩达到2.30m属于优秀,那么优秀率是多少?试估算全校男生立定跳远优秀的人数.19. 如图,在△ABC中,D、E分别是AB,AC上的点,∠AED=∠B,△ABC用平分线AF交DE于点G,交BC于点F. (1)、求证:△AED∽△ABC.(2)、设 ,求 的值.20. 已知点A(﹣2,a),B(﹣1,b),C(3,c)都在反比例函数y= (k≠0)的图象上.(1)、若b=a+1,求c的值.(2)、若a>b,试比较b,c的大小关系,并说明理由.21. 如图,在正方形ABCD中,点E,F分别在边AD,CD上,且AE=DF,连接并延长AF,分别交BE于点G,BC延长线于点H.
(1)、求证:△AED∽△ABC.(2)、设 ,求 的值.20. 已知点A(﹣2,a),B(﹣1,b),C(3,c)都在反比例函数y= (k≠0)的图象上.(1)、若b=a+1,求c的值.(2)、若a>b,试比较b,c的大小关系,并说明理由.21. 如图,在正方形ABCD中,点E,F分别在边AD,CD上,且AE=DF,连接并延长AF,分别交BE于点G,BC延长线于点H. (1)、请判断BE与AF的位置关系,并说明理由.(2)、连接EH,若EB=EH,求证BG=2GE.
(1)、请判断BE与AF的位置关系,并说明理由.(2)、连接EH,若EB=EH,求证BG=2GE.
