浙江省杭州市拱墅区六校2021年数学中考二模联考试卷

试卷更新日期：2021-09-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算7x﹣3x的结果是（）

A、4x B、4 C、﹣4x D、﹣4

查看试题解析
2. 今年“五一”小长假期间，杭州市各景区景点共接待市民游客大约9210000人次，与去年同期相比增长85%.数据9210000用科学记数法表示为（）

A、92.1×10⁵ B、921×10⁴ C、9.21×10⁶ D、9.21×10⁷

查看试题解析
3. 如图， $a // b$ ，若∠1＝2∠2，则∠2的度数为（）

A、50° B、60° C、70° D、80°

查看试题解析
4. 要使分式 $\frac{1}{x - 1}$ 有意义，则x的取值范围是（）

A、 $x > 1$ B、 $x \neq 1$ C、 $x = 1$ D、 $x \neq 0$

查看试题解析
5. 已知a＜b，则（）

A、a+1＜b+2 B、a﹣1＞b﹣2 C、ac＜bc D、 $\frac{a}{c} > \frac{b}{c}$

查看试题解析
6. 某玩具厂质检员对A，B，C，D，E这5个玩具进行称重，实际重量分别为：90，87，92，92，91（单位：克）.在统计时，不小心将B玩具的重量写成了90克，则计算结果不受影响的是（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
7. 如图，破残的轮子上，弓形的弦AB为4m，高CD为1m，则这个轮子的半径长为（）

A、 $\sqrt{17}$ m B、 $\sqrt{5}$ m C、5m D、 $\frac{5}{2}$ m

查看试题解析
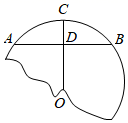8. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”意思是：用一根绳子去量一根木条，绳子还剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?如果设木条长x尺，绳子长y尺，那么可列方程组为（）

A、 ${\begin{cases} y = x + 4.5 \\ 0.5 y = x - 1 \end{cases}$ B、 ${\begin{cases} y = x + 4.5 \\ y = 2 x - 1 \end{cases}$ C、 ${\begin{cases} y = x - 4.5 \\ 0.5 y = x + 1 \end{cases}$ D、 ${\begin{cases} y = x - 4.5 \\ y = 2 x - 1 \end{cases}$

查看试题解析
9. 图1是某公园的一个滑梯，图2是其示意图.滑梯的高BC为2m，坡角∠A为60°，由于滑梯坡角过大存在安全隐忠，公园管理局决定对滑梯进行整改，要在高度不变的前提下，通过加长滑梯的水平距离AB，使得坡角∠A满足30°≤∠A≤45°，则AB加长的距离可以是（）
（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

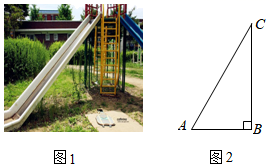A、0.8m B、1.6m C、2.4m D、3.2m

查看试题解析
10. 已知二次函数y＝﹣（x﹣1）²+10，当m≤x≤n，且mn＜0时，y的最小值为2m，y的最大值为2n，则 $m + n$ 的值为（）

A、3 B、 $\frac{5}{2}$ C、2 D、 $\frac{3}{2}$

查看试题解析

二、填空题

11. 二次根式 $\sqrt{x}$ 中字母x的取值范围是.

查看试题解析
12. 已知 $a + b = 3$ ，a﹣b＝1，则a²﹣b²＝.

查看试题解析
13. 已知一个圆锥的底面半径为12cm，母线长为20cm，则这个圆锥的侧面积为.

查看试题解析
14. 一个布袋里装有只有颜色不同的5个球，其中3个红球，2个白球.从中任意摸出1个球，记下颜色后放回，搅匀，再任意摸出1个球，摸出的2个球都是红球的概率是.

查看试题解析
15. A城有种农机30台，B城有该农机40台，现要将这些农机全部运往C，D两乡，调运任务承包给某运输公司.已知C乡需要农机34台，D乡需要农机36台，从A城往C，D两乡运送农机的费用分别为250元/台和200元/台，从B城往C，D两乡运送农机的费用分别为150元/台和240元/台.设A城运往C乡该农机x台，运送全部农机的总费用为W元，则W关于x的函数关系式为.

查看试题解析
16. 如图，在正方形ABCD中，以CD为边向形内作等边三角形CDG，连接AG，点E和F在边CD上，连接AE，BF，分别交DG，CG于点M，N，连接MN，则∠AGD＝，若∠DAE＝∠CBF＝15°，则 $\frac{M N}{C D}$ ＝.

查看试题解析

三、解答题

17.

(1)、计算：|﹣2|+3^﹣1；

(2)、解方程：x²﹣2x﹣15＝0.

查看试题解析
18. 为了解某校学生对球类运动的喜爱情况，调查小组就打排球、打乒乓球、打篮球、踢足球四项球类运动对该校学生进行了“你最喜爱的球类运动”的抽样调查，并根据调查结果绘制成如下统计图.

(1)、本次抽样调查的样本容量是；

(2)、补全条形统计图；

(3)、该校共有2000名学生，请你估计该校最喜爱“打篮球”的学生人数.

查看试题解析
19. 如图，在△ABC中，D，E分别是AB，AC上的点，△ADE∽△ACB.△ABC的角平分线AF交DE于点G，交BC于点F.

(1)、求证：△ADG∽△ACF；

(2)、若AE：AB＝2：3，求 $\frac{A G}{F G}$ 的值.

查看试题解析
20. 五一假期，小夏驾驶小汽车匀速地从杭州行驶到宁波，当小汽车行驶的速度为每小时100千米时，行驶时间1.5小时.设小汽车行驶的速度为v千米/时，行驶的时间为t小时，全程速度限定为不超过120千米/小时.

(1)、求v关于t的函数表达式；

(2)、若小汽车行驶的速度为50千米/时，则从杭州到宁波需要几小时？

(3)、若小夏下午4点从杭州出发，他能在下午5：10到达宁波吗？请说明理由.

查看试题解析
21. 如图，在菱形ABCD中，对角线AC，BD相交于点O，AB＝6，sin∠DBC＝ $\frac{1}{3}$ .

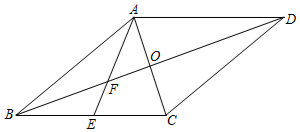(1)、求对角线BD的长；

(2)、若E是BC的中点，连接AE，交BD于点F，求△BEF的面积.

查看试题解析
22. 设二次函数y＝x²﹣2（m+1）x+3﹣m，其中m是实数.

(1)、若函数的图象经过点（﹣2，8），求此函数的表达式；

(2)、若x＞0时，y随x的增大而增大，求m的最大值.

(3)、已知A（﹣1，3），B（2，3），若该二次函数的图象与线段AB只有一个交点（不包括A，B两个端点），求m的取值范围.

查看试题解析
23. 如图，以△ABC的一边AB为直径作⊙O，交BC于点D，交AC于点E，点D为 $\overset{⌢}{B E}$ 的中点.

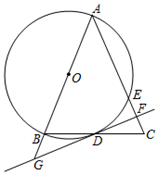(1)、试判断△ABC的形状，并说明理由；

(2)、直线l切⊙O于点D，与AC及AB的延长线分别交于点F，点G.
①若∠BAC＝45°，求 $\frac{D F}{D G}$ 的值；

②若⊙O半径的长为r，△ABC的面积为△CDF的面积的12倍，求BG的长（用含r的代数式表示）.

查看试题解析