湖南省株洲市渌口区2021年数学中考模拟试卷

试卷更新日期：2021-09-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，比﹣2小的数是（）

A、﹣3 B、﹣1.5 C、﹣1 D、2

查看试题解析
2. 计算 ${(- a)}^{6} \div a^{3}$ 的结果是（）

A、 $- a^{3}$ B、 $- a^{2}$ C、 $a^{3}$ D、 $a^{2}$

查看试题解析
3. 如图，AB和CD相交于点O，则下列结论正确的是（）

A、∠1＞∠4+∠5 B、∠2＝∠3+∠5 C、∠1＝∠2 D、∠2＜∠5

查看试题解析
4. 如图，点A，B，C均在⊙O上，若∠A＝64°，则∠OCB的度数是（）

A、24° B、26° C、28° D、30°

查看试题解析
5. 若点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称，则m+n的值是（）

A、﹣5 B、﹣3 C、3 D、1

查看试题解析
6. 如图所示，圆柱的高AB＝3，底面直径BC＝6，现在有一只蚂蚁想要从A处沿圆柱侧面爬到对角C处捕食，则它爬行的最短距离是（）

A、3 $\sqrt{1 + π^{2}}$ B、6 $\sqrt{1 + π^{2}}$ C、9 D、6 $\sqrt{2}$

查看试题解析
7. 已知一次函数y＝kx+4的图象经过点A，且y随x的增大而减小，则点A的坐标不会是（）

A、（﹣2，﹣5） B、（﹣1，6） C、（﹣2，6） D、（1，3）

查看试题解析
8. 若式子 $\sqrt{2 x - 4}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x \neq 2$ B、 $x \geq 2$ C、 $x \leq 2$ D、 $x \neq - 2$

查看试题解析
9. 如果x²+nx+2k＝（x﹣1）² ，那么kⁿ是（）

A、﹣ $\frac{1}{4}$ B、 $\frac{1}{4}$ C、4 D、﹣4

查看试题解析
10. 将边长分别为2、3、5的三个正方形按如图方式排列，则图中阴影部分的面积为（）

A、 $\frac{15}{2}$ B、 $\frac{15}{3}$ C、 $\frac{15}{4}$ D、3

查看试题解析

二、填空题

11. 已知f（x）＝ $\frac{2}{x - 1}$ ，那么f（5）的值是.

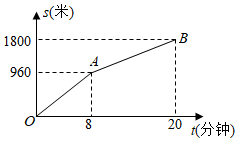
查看试题解析
12. 计算： $\sqrt{9} - 5$ ＝.

查看试题解析
13. 分解因式xy²—x=.

查看试题解析
14. 为了解某区六年级8400名学生中会游泳的学生人数，随机调查了其中400名学生，结果有150名学生会游泳，那么估计该区会游泳的六年级学生人数约为．

查看试题解析
15. 已知 $α$ ， $β$ 是一元二次方程 $x^{2} + x - 2 = 0$ 的两个实数根，则 $α + β - α β$ 的值是.

查看试题解析
16. 小李从家步行到学校需走的路程为1800米.图中的折线OAB反映了小李从家步行到学校所走的路程s（米）与时间t（分钟）的函数关系，根据图象提供的信息，当小李从家出发去学校步行16分钟时，到学校还需步行米.

查看试题解析
17. 把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上.若AB= $\sqrt{2}$ ，则CD=.

查看试题解析
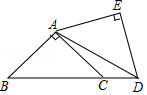18. Rt△ABC中，∠ABC=90°，AB=3，BC=4，过点B的直线把△ABC分割成两个三角形，使其中只有一个是等腰三角形，则这个等腰三角形的面积是．

查看试题解析

三、解答题

19. 计算： ${(\frac{1}{2})}^{- 1} - 2 \sin 45 ° + | - \sqrt{2} | + {(2021 - π)}^{0}$

查看试题解析
20. 先化简，再求值 $\frac{2 m + 1}{m}$ ÷ $\frac{m^{2} - 1}{m}$ ，其中m＝ $\sqrt{3}$ +1.

查看试题解析
21. 如图，在△ABC中，AB＝8，BC＝4，CA＝6，CD//AB，BD是∠ABC的平分线，BD交AC于点E，求AE的长.

查看试题解析
22. 为响应党的“文化自信”号召，某校开展了古诗词诵读大赛活动，现随机抽取部分同学的成绩进行统计，并绘制成两个不完整的统计图，请结合图中提供的信息，解答下列各题：

(1)、直接写出a的值，a＝ ▲ ，并把频数分布直方图补充完整.

(2)、求扇形B的圆心角度数.

(3)、如果全校有2700名学生参加这次活动，90分以上（含90分）为优秀，那么估计获得优秀奖的学生有多少人？

查看试题解析
23. 某区域平面示意图如图，点O在河的一侧，AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°，乙勘测员在B处测得点O位于南偏西73.7°，测得AC=840m，BC=500m.请求出点O到BC的距离.参考数据：sin73.7°≈ $\frac{24}{25}$ ，cos73.7°≈ $\frac{7}{25}$ ，tan73.7°≈ $\frac{24}{7}$

查看试题解析
24. 如图，点O是△ABC的边AB上一点，⊙O与边AC相切于点E，与边BC，AB分别相交于点D，F，且DE=EF，

(1)、求证：∠C=90°；

(2)、当BC=3，sinA= $\frac{3}{5}$ 时，求AF的长.

查看试题解析
25. 已知反比例函数的图象经过三个点A（﹣4，﹣3），B（2m，y₁），C（6m，y₂），其中m＞0.

(1)、当y₁﹣y₂=4时，求m的值；

(2)、如图，过点B、C分别作x轴、y轴的垂线，两垂线相交于点D，点P在x轴上，若三角形PBD的面积是8，请写出点P坐标（不需要写解答过程）.

查看试题解析
26. 已知抛物线y=ax²+bx+c过点A（0，2）．

(1)、若点（﹣ $\sqrt{2}$ ，0）也在该抛物线上，求a，b满足的关系式；

(2)、若该抛物线上任意不同两点M（x₁ ， y₁），N（x₂ ， y₂）都满足：当x₁＜x₂＜0时，（x₁﹣x₂）（y₁﹣y₂）＞0；当0＜x₁＜x₂时，（x₁﹣x₂）（y₁﹣y₂）＜0．以原点O为心，OA为半径的圆与拋物线的另两个交点为B，C，且△ABC有一个内角为60°．
①求抛物线的解析式；
②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．

查看试题解析