广西柳州市柳江区2021年数学中考模拟试卷（5月）

试卷更新日期：2021-09-24 类型：中考模拟

进入出卷网下载

一、单选题

1. -3相反数是（）

A、 $\frac{1}{3}$ B、-3 C、 $- \frac{1}{3}$ D、3

查看试题解析
2. 如图是一个几何体的三视图，则这个几何体是（）．

A、三棱锥 B、圆锥 C、三棱柱 D、圆柱

查看试题解析
3. 计算 $3 - (- 2)$ 的结果是（）

A、-5 B、-1 C、1 D、5

查看试题解析
4. “扶贫”是新时期党和国家的重点工作之一，为落实习近平总书记提出的“精准扶贫”战略构想，某省预计三年内脱贫1020000人，数字1020000用科学记数法可表示为（）

A、1.02×10⁶ B、1.02×10⁵ C、10.2×10⁵ D、102×10⁴

查看试题解析
5. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 下列运算中，正确的是（）

A、 $a (- a) = - a^{2}$ B、 $a (a + 1) = a^{2} + 1$ C、 $2 a - a = 1$ D、 $a^{2} + a = 3 a$

查看试题解析
7. 已知a＝b，下列变形不正确的是（）

A、a+5＝b+5 B、a﹣5＝b﹣5 C、5a＝5b D、 $\frac{a}{c} = \frac{b}{c}$

查看试题解析
8. 不等式组 ${\begin{array}{l} x + 2 > 0 \\ - 2 x + 4 \geq 0 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
9. 一个不透明的盒子中装有4个形状、大小质地完全相同的小球，这些小球上分别标有数字-1、0、2和3．从中随机地摸取一个小球，则这个小球所标数字是正数的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
10. 下列四种基本尺规作图分别表示，则对应选项中作法错误的是（）

A、作一个角等于已知角 B、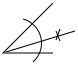作一个角的平分线 C、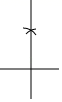作一条线段的垂直平分线 D、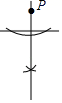过直线外一点P作已知直线的垂线

查看试题解析
11. 如图， $P$ 是 $⊙ O$ 外一点，PA，PB分别切 $⊙ O$ 于点A，B，点C在优弧 $\overset{⌢}{A B}$ 上，若 $∠ P = 68 °$ ，则 $∠ A C B$ 等于（）

A、68° B、34° C、112° D、56°

查看试题解析
12. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2021次运动后，动点P的坐标是（）

A、 $(2021 ， 0)$ B、 $(2021 ， 1)$ C、 $(2021 ， 2)$ D、 $(2021 ， 505)$

查看试题解析

二、填空题

13. 若二次根式 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
14. 对于实数 $a$ ， $b$ ，定义一种新运算“ $\otimes$ ”为： $a \otimes b = \frac{1}{a - b^{2}}$ ，这里等式右边是实数运算.例如： $1 \otimes 3 = \frac{1}{1 - 3^{2}} = - \frac{1}{8}$ .则方程 $x \otimes (- 2) = 1$ 的解是.

查看试题解析
15. 如图，直线a，b被直线c所截，且a∥b，∠1=40°，则∠2=度.

查看试题解析
16. 如图，在平面直角坐标系中，四边形 $A B O C$ 为平行四边形， $A (1 ， 2)$ ， $B (3 ， 1)$ ，且点C在反比例函数 $y = \frac{k}{x}$ 的图象上，则k的值为.

查看试题解析
17. 如图所示，点A、B、C对应的刻度分别为0、2、4，将线段CA绕点C按顺时针方向旋转，当点A首次落在矩形BCDE的边BE上时，记为点A₁ ，则此时线段CA扫过的图形的面积为.

查看试题解析
18. 如图，对折矩形纸片ABCD，使得AD与BC重合，得折痕MN，再把纸片展平，E是AD上一点，将 $△ A B E$ 沿BE折叠，使点A的对应点 $A^{'}$ 落在MN上，若 $C D = 6$ ，则BE的长是.

查看试题解析

三、解答题

19. 计算： ${(\frac{1}{4})}^{- 1} + \sqrt[3]{8} - \sqrt{3} \tan 60 °$ .

查看试题解析
20. 已知；如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点 $E$ 是 $A B$ 的中点，若 $A N = \frac{1}{2} A B$ ， $A N // C E$ .
求证： $A C = N E$

查看试题解析
21. 先化简： $(\frac{x}{x - 1} - 1) \div \frac{x^{2} - x}{x^{2} - 2 x + 1}$ ，然后从 $- 1 \leq x \leq 3$ 中选一个你认为适合的整数 $x$ 代入求值.

查看试题解析
22. 今年5月9日母亲节那天，某班很多同学给妈妈准备了鲜花和礼盒，请根据图中的信息回答问题：

(1)、求一束鲜花和一个礼盒的价格；

(2)、若小强给妈妈买了一束鲜花和一个礼盒，小强一共花了多少钱?

查看试题解析
23. 某校物理实验小组随机抽取了部分学生的物理实验测试成绩进行调查，调查结果只有三个分数；1分（合格），2分（良好），3分（优秀），并将调查结果绘制成如下两幅不完整的统计图图1和图2，请回答下列问题：

(1)、这次被调查的学生共有 ▲ 人，并将条形统计图补充完整；

(2)、这次被调查学生物理实验测试成绩的众数是，中位数是；

(3)、小聪奇思妙想将上图的扇形统计图做成了如图3所示的一个转盘，随机转动两次转盘（指针指向边界不计），求两次指针所指数字之和为奇数的概率.

查看试题解析
24. 如图，已知 $A (- 4 ， \frac{1}{2}) ， B (- 1 ， m)$ 是一次函数 $y = k x + b$ 与反比例函数 $y = - \frac{2}{x} (x < 0)$ 图象的两个交点， $A C ⊥ x$ 轴于 $C ， B D ⊥ y$ 轴于 $D$ .

(1)、求一次函数解析式及 $m$ 的值；

(2)、 $P$ 是线段 $A B$ 上的一点，连接 $P C ， P D ，$ 若 $△ P C A$ 和 $△ P D B$ 面积相等，求点 $P$ 坐标.

查看试题解析
25. 如图，△ABC内接于⊙O，且AB为⊙O的直径.∠ACB 的平分线交⊙O于点D，过点D作直线l交CA的延长线于点P，且∠ADP=∠BCD，过点A作AE丄CD于点E，过点B作BF丄CD于点F.

(1)、求证：DP//AB；

(2)、求证：PD是⊙O的切线；

(3)、若AC=6，BC=8，求线段PD的长.

查看试题解析
26. 如图，抛物线 $y = - x^{2} + b x + c$ 经过点 $A (- 4 ， - 4)$ ， $B (0 ， 4)$ ，直线AC的解析式为 $y = - \frac{1}{2} x - 6$ ，且与y轴相交于点C，若点E是直线AB上的一个动点，过点E作 $E F ⊥ x$ 轴交AC于点F.

(1)、求抛物线 $y = - x^{2} + b x + c$ 的解析式；

(2)、点H是y轴上一动点，连结EH，HF，当点E运动到什么位置时，四边形EAFH是矩形?求出此时点E，H的坐标；

(3)、在（2）的前提下，以点E为圆心，EH长为半径作圆，点M为 $⊙ E$ 上以动点，求 $\frac{1}{2} A M + C M$ 的最小值.

查看试题解析