广西岑溪市2021年九年级数学第二次抽样调研测试试卷
试卷更新日期:2021-09-24 类型:中考模拟
一、单选题
-
1. -2021的相反数是( )A、-2021 B、 C、 D、20212. 如图所示,直线a、b被直线c所截,∠1与∠2是( )
 A、内错角 B、同位角 C、同旁内角 D、邻补角3. 观察下列立体图形,左视图为矩形的是( )A、
A、内错角 B、同位角 C、同旁内角 D、邻补角3. 观察下列立体图形,左视图为矩形的是( )A、 B、
B、 C、
C、 D、
D、 4. 2021年1月20日0时25分,我国在西昌卫星发射中心用长征三号乙运载火箭,成功将天通一号03星发射升空.卫星顺利进入预定轨道,任务获得圆满成功,天通一号在接近36000公里的地球同步轨道上运行,其中数据36000用科学记数法可表示为( )A、 B、 C、 D、5. 不等式3x-2>4的解集在数轴上表示正确的是( )A、
4. 2021年1月20日0时25分,我国在西昌卫星发射中心用长征三号乙运载火箭,成功将天通一号03星发射升空.卫星顺利进入预定轨道,任务获得圆满成功,天通一号在接近36000公里的地球同步轨道上运行,其中数据36000用科学记数法可表示为( )A、 B、 C、 D、5. 不等式3x-2>4的解集在数轴上表示正确的是( )A、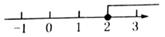 B、
B、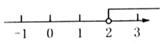 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 以下调查中,最适合采用抽样调查的是( )A、2020年11月1日实施的全国人口普查 B、了解一批灯泡的使用寿命 C、疫情期间,返校前某班学生的日常体温 D、调查乘坐飞机的旅客是否携带了危禁物品8. 下列关于抛物线 的说法正确的是( )A、抛物线开口向上 B、顶点坐标为 C、在对称轴的右侧, 随 的增大而增大 D、抛物线与 轴有两个交点9. 主题为“绿色城市、健康生活”的世界园艺博览会将于2021年4月至10月在枣林湾举行.世园会的某纪念品受到热烈欢迎,从原价50元连续两次涨价达到72元,如果每次涨价的百分率都是x,则下面所列方程正确的是( )A、 B、 C、 D、10. 一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点 落在反比例函数 图象上的概率为( )A、 B、 C、 D、11. 如图 是 切线,点A为切点, 交 于点C , 点D在 上,连接 ,若 ,则 的度数为( )
6. 下列运算正确的是( )A、 B、 C、 D、7. 以下调查中,最适合采用抽样调查的是( )A、2020年11月1日实施的全国人口普查 B、了解一批灯泡的使用寿命 C、疫情期间,返校前某班学生的日常体温 D、调查乘坐飞机的旅客是否携带了危禁物品8. 下列关于抛物线 的说法正确的是( )A、抛物线开口向上 B、顶点坐标为 C、在对称轴的右侧, 随 的增大而增大 D、抛物线与 轴有两个交点9. 主题为“绿色城市、健康生活”的世界园艺博览会将于2021年4月至10月在枣林湾举行.世园会的某纪念品受到热烈欢迎,从原价50元连续两次涨价达到72元,如果每次涨价的百分率都是x,则下面所列方程正确的是( )A、 B、 C、 D、10. 一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点 落在反比例函数 图象上的概率为( )A、 B、 C、 D、11. 如图 是 切线,点A为切点, 交 于点C , 点D在 上,连接 ,若 ,则 的度数为( ) A、 B、 C、 D、12. 如图,已知点C在以 为直径,O为圆心的半圆上, ,以 为边作等边 ,则 的最大值是( )
A、 B、 C、 D、12. 如图,已知点C在以 为直径,O为圆心的半圆上, ,以 为边作等边 ,则 的最大值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 因式分解: .
14. 一组数据:2、4、4、3、7、7,则这组数据的中位数是.15. 计算: .16. 如图, 中,对角线 、 相交于点O, 交 于点E,连接 ,若 的周长为28,则 的周长为. 17. 如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为.
17. 如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为. 18. 如图,点N是反比例函数 图象上的一个动点,过点N作 轴,交直线 于点M,则 面积的最小值是.
18. 如图,点N是反比例函数 图象上的一个动点,过点N作 轴,交直线 于点M,则 面积的最小值是.
三、解答题
-
19. 计算: .20. 解方程: + =1.21. 如图,在平面直角坐标系中,已知 三个顶点的坐标分别是 , , .

( 1 )画出 向左平移6个单位长度后得到的 ;
( 2 )以点 为位似中心,将 缩小为原来的 ,得到 ,请在y轴右侧画出 ,并直接写 的值.
(不写解答过程,直接写结果,保留作图痕迹.)
22. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行,在A处测得灯塔P在北偏东 方向上,继续航行30分钟后到达 处,此时测得灯塔P在北偏东 方向上.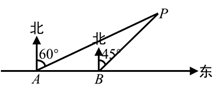 (1)、求 的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?(参考数据: , )23. 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
(1)、求 的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?(参考数据: , )23. 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.组别
成绩x(分)
频数(人数)
A
8.0≤x<8.5
a
B
8.5≤x<9.0
8
C
9.0≤x<9.5
15
D
9.5≤x<10
3
 (1)、图中a= , 这次比赛成绩的众数落在组;(2)、请补全频数分布直方图;(3)、学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.24. 某中学开学初到商场购买A、B两种品牌的足球,购买A种品牌的足球20个,B种品牌的足球30个,共花费4600元,已知购买4个B种品牌的足球与购买5个A种品牌的足球费用相同.
(1)、图中a= , 这次比赛成绩的众数落在组;(2)、请补全频数分布直方图;(3)、学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.24. 某中学开学初到商场购买A、B两种品牌的足球,购买A种品牌的足球20个,B种品牌的足球30个,共花费4600元,已知购买4个B种品牌的足球与购买5个A种品牌的足球费用相同.
(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元.
(2)、学校为了响应习总书记“足球进校园”的号召,决定再次购进A、B两种品牌足球共42个,正好赶上商场对商品价格进行调整,A品牌足球售价比第一次购买时提高5元,B品牌足球按第一次购买时售价的9折出售,如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的80%,且保证这次购买的B种品牌足球不少于20个,则这次学校有哪几种购买方案?
(3)、请你求出学校在第二次购买活动中最多需要多少资金?25. 如图,直线 与 相离,过点 作 ,垂足为 , 交 于点 .点 在直线 上,连接 并延长交 于点 ,在直线 上另取一点 ,使 . (1)、求证: 是 的切线;(2)、已知 , , .
(1)、求证: 是 的切线;(2)、已知 , , .①求 的半径 ;
②求 的面积.
26. 如图,抛物线 交 轴于点 、 ,交 轴于点 ,点的 坐标为(3,0),点的 坐标为(0,3),点 与点 关于抛物线的对称轴对称. (1)、求抛物线的解析式;(2)、若点 为抛物线对称轴上一动点,连接 ,以 、 为边作平行四边形 ,是否存在这样的点 ,使平行四边形 是矩形?若存在,请求出点 的坐标;(3)、在(2)的结论下,求出 的值.
(1)、求抛物线的解析式;(2)、若点 为抛物线对称轴上一动点,连接 ,以 、 为边作平行四边形 ,是否存在这样的点 ,使平行四边形 是矩形?若存在,请求出点 的坐标;(3)、在(2)的结论下,求出 的值.