甘肃省天水市麦积区2021年数学中考模拟试卷
试卷更新日期:2021-09-24 类型:中考模拟
一、单选题
-
1. 计算﹣ ﹣|﹣3|的结果是( )A、﹣1 B、5 C、1 D、-52. 如图是某个几何体的展开图,该几何体是( )
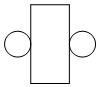 A、圆锥 B、圆柱 C、圆台 D、四棱柱3. 2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数128 000 000 000 000用科学记数法表示为( )A、1.28 1014 B、1.28 10-14 C、128 1012 D、0.128 10114. 一组数据:5,7,10,5,7,5,6,这组数据的众数和中位数分别是( )A、10和7 B、5和7 C、6和7 D、5和65. 圆锥底面圆的半径为3cm,其侧面展开图是半圆,则圆锥母线长为()A、3cm B、6cm C、9cm D、12cm6. 如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )
A、圆锥 B、圆柱 C、圆台 D、四棱柱3. 2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数128 000 000 000 000用科学记数法表示为( )A、1.28 1014 B、1.28 10-14 C、128 1012 D、0.128 10114. 一组数据:5,7,10,5,7,5,6,这组数据的众数和中位数分别是( )A、10和7 B、5和7 C、6和7 D、5和65. 圆锥底面圆的半径为3cm,其侧面展开图是半圆,则圆锥母线长为()A、3cm B、6cm C、9cm D、12cm6. 如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )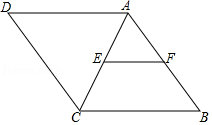 A、24 B、18 C、12 D、97. 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD= ,则S阴影=( )
A、24 B、18 C、12 D、97. 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD= ,则S阴影=( ) A、2π B、 π C、 π D、 π8. 函数y1=x和y2= 的图象如图所示,则y1>y2的x取值范围是( )
A、2π B、 π C、 π D、 π8. 函数y1=x和y2= 的图象如图所示,则y1>y2的x取值范围是( )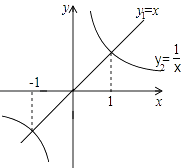 A、x<﹣1或x>1 B、x<﹣1或0<x<1 C、﹣1<x<0或x>1 D、﹣1<x<0或0<x<19. 如图,小正方形是按一定规律摆放的,下面四个选项中的图片,适合填补图中空白处的是( )
A、x<﹣1或x>1 B、x<﹣1或0<x<1 C、﹣1<x<0或x>1 D、﹣1<x<0或0<x<19. 如图,小正方形是按一定规律摆放的,下面四个选项中的图片,适合填补图中空白处的是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 在物理实验课上,老师用弹簧秤将铁块悬于盛有水的水槽中,然后匀速向上提起,直到铁块完全露出水面一定高度,则下图能反映弹簧秤的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )
10. 在物理实验课上,老师用弹簧秤将铁块悬于盛有水的水槽中,然后匀速向上提起,直到铁块完全露出水面一定高度,则下图能反映弹簧秤的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( ) A、
A、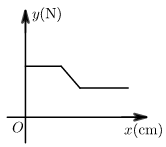 B、
B、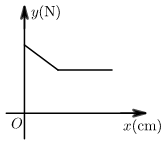 C、
C、 D、
D、
二、填空题
-
11. 因式分解: .
12. 不等式组 的解集为13. 某班50名学生在2018年适应性考试中,数学成绩在100〜110分这个分数段的频率为0.2,则该班在这个分数段的学生为人.
14. 反比例函数 (k是常数,k≠0)的图象经过点(1,4),那么这个函数图象所在的每个象限内,y的值随x值的增大而.(填“增大”或“减小”)15. 若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根,则m的值为 .16. 如图所示,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=5,则这个梯形中位线的长等于. 17. 已知△ABC的边BC=4cm,⊙O是其外接圆,且半径也为4cm,则∠A的度数是 .18. 如图,一段抛物线y=﹣x(x﹣1)(0≤x≤1)记为m1 , 它与x轴交点为O、A1 , 顶点为P1;将m1绕点A1旋转180°得m2 , 交x轴于点A2 , 顶点为P2;将m2绕点A2旋转180°得m3 , 交x轴于点A3 , 顶点为P3 , …,如此进行下去,直至得m10 , 顶点为P10 , 则P10的坐标为.
17. 已知△ABC的边BC=4cm,⊙O是其外接圆,且半径也为4cm,则∠A的度数是 .18. 如图,一段抛物线y=﹣x(x﹣1)(0≤x≤1)记为m1 , 它与x轴交点为O、A1 , 顶点为P1;将m1绕点A1旋转180°得m2 , 交x轴于点A2 , 顶点为P2;将m2绕点A2旋转180°得m3 , 交x轴于点A3 , 顶点为P3 , …,如此进行下去,直至得m10 , 顶点为P10 , 则P10的坐标为.
三、解答题
-
19.(1)、计算:(﹣1)2021﹣2﹣1+sin30°+(π﹣3.14)0(2)、先化简,再求值:(x+1)(x﹣1)+(2x﹣1)2﹣2x(2x﹣1),其中x= +120. 如图,一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
 21. 如图,在平面直角坐标系 中,函数 的图象与直线 交于点A( ).B( )两点.
21. 如图,在平面直角坐标系 中,函数 的图象与直线 交于点A( ).B( )两点. (1)、求 的值;(2)、连结OA,点P是函数 上一点,且满足OP=OA,直接写出点P的坐标(点A除外).(3)、连结OB,求△AOB的面积.22. 2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化.某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图.请你根据图中提供的信息完成下列问题:
(1)、求 的值;(2)、连结OA,点P是函数 上一点,且满足OP=OA,直接写出点P的坐标(点A除外).(3)、连结OB,求△AOB的面积.22. 2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化.某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图.请你根据图中提供的信息完成下列问题: (1)、求被调查学生的人数,并将条形统计图补充完整;(2)、求扇形统计图中的A等对应的扇形圆心角的度数;(3)、已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?23. 如图,CD是⊙O的切线,点C在直径AB的延长线上.
(1)、求被调查学生的人数,并将条形统计图补充完整;(2)、求扇形统计图中的A等对应的扇形圆心角的度数;(3)、已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?23. 如图,CD是⊙O的切线,点C在直径AB的延长线上. (1)、求证:∠CAD=∠BDC;
(1)、求证:∠CAD=∠BDC;
(2)、若BD= AD,AC=3,求CD的长.
24. 某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)、求甲、乙两种树苗每棵的价格各是多少元?
(2)、在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?

