福建省南平市2021年数学初中毕业班综合练习（一）

试卷更新日期：2021-09-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数2021的相反数是（）

A、2021 B、-2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
2. 如图是某几何体的视图，该几何体是（）

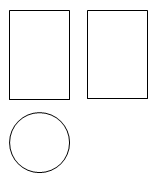A、圆柱 B、球 C、三棱柱 D、长方体

查看试题解析
3. 2020年6月23日，北斗三号最后一颗全球组网卫星从西昌卫星发射中心发射升空，6月30日成功定点于距离地球36002公里的地球同步轨道．将36000用科学记数法表示应为（）

A、 ${\begin{matrix} 0.36 \times 10 \end{matrix}}^{5}$ B、 $3.6 \times 10^{5}$ C、 $3.6 \times 10^{4}$ D、 $36 \times 10^{3}$

查看试题解析
4. 下列垃圾分类标识的图案既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 灿灿妈妈在网上销售装饰品.最近五天，每天销售某种装饰品的个数为：9，12，13，12，14.灿灿对这组数据的分析，其中错误的是（）

A、众数是12 B、平均数是12 C、方差是 $\frac{14}{5}$ D、中位数是13

查看试题解析
6. 实数 $a ， b$ 在数轴上表示的位置如图所示，则（）

A、 $a > b$ B、 $| a | < | b |$ C、 $a + b < 0$ D、 $a - b > 0$

查看试题解析
7. 如图，函数 $y = k x + b$ 经过点 $A (- 3 ， 2)$ ，则关于x的不等式 $k x + b < 2$ 的解集为（）

A、 $x > - 3$ B、 $x < - 3$ C、 $x > 2$ D、 $x < 2$

查看试题解析
8. 如图，点A、B、C在⊙O上，∠ABC＝45°，连接AO，过点O作OE⊥BC交BC于点D，交⊙O于点E.若点D是OE的中点，则∠AOE的度数为（）

A、160° B、150° C、135° D、120°

查看试题解析
9. 数学中，把宽与长之比为 $\frac{\sqrt{5} - 1}{2} (\frac{\sqrt{5} - 1}{2} \approx 0.618)$ 的矩形称为黄金矩形，这个比例 $\frac{\sqrt{5} - 1}{2}$ 被称为黄金分割比例.如图，名画《蒙娜丽莎的微笑》的整个画面的主体部分很好地体现了黄金分割比例，其中矩形ABCD是黄金矩形，若我们把一个正方形AEFD嵌入黄金矩形ABCD中（正方形的边长等于黄金矩形的宽），这样就创造了一个新的黄金矩形BEFC.如果把这个过程重复数次，接着我们要在每个正方形内画一条圆弧，让每个圆弧的半径等于它所在正方形的边长就会得到下面这张图，若 $A B = a$ ，则图中弧HF的长为（）

A、 $\frac{\sqrt{5} - 1}{2} a$ B、 $\frac{π}{2} • \frac{\sqrt{5} - 1}{2} a$ C、 $\frac{π}{2} • {(\frac{\sqrt{5} - 1}{2})}^{2} a$ D、 $\frac{π}{2} • {(\frac{\sqrt{5} - 1}{2})}^{3} a$

查看试题解析
10. 在平面直角坐标系中，设二次函数 $y = (x - a) (x + a + 1) (a \neq 0)$ ，已知点 P(p，m)和 Q(1， n)在二次函数的图象上，若 m ＜n，则 p 的取值范围为（）

A、 $p < - 2$ B、 $- 2 < p < a$ C、 $- 2 < p < 1$ D、 $p > 1$

查看试题解析

二、填空题

11. 使代数式 $\sqrt{x - 1}$ 有意义的x的取值范围是．

查看试题解析
12. 为了估计湖里有多少条鱼，有如下方案：从湖里捕上100条鱼做上标记，然后放回湖里，经过一段时间，待带标记的鱼完全混合于鱼群后，第二次再捕上200条，若其中带有标记的鱼有10条，那么估计湖里大约有条鱼．

查看试题解析
13. 点P（a ， b）在函数y＝3x+2的图象上，则代数式6a﹣2b+1的值等于．

查看试题解析
14. 我国古代数学名著《孙子算经》中记载了一道题，大意是： $100$ 匹马恰好拉了 $100$ 片瓦，已知 $3$ 匹小马能拉 $1$ 片瓦， $1$ 匹大马能拉片 $3$ 瓦，求小马、大马各有多少匹.若设小马有x匹，大马有y匹，依题意，可列方程组为．

查看试题解析
15. 如图，正五边形 $A B C D E$ 的边长为2，以 $A B$ 为边作等边 $△ A B F$ ，则图中阴影部分的面积为.

查看试题解析
16. 如图，点 $A$ 是双曲线 $y = \frac{5}{x}$ 上的一个动点，连接 $A O$ 并延长交双曲线于点 $B ，$ 将线段 $A B$ 绕点 $B$ 逆时针旋转 $60 °$ 得到线段 $B C ，$ 若点 $C$ 在双曲线 $y = \frac{k}{x} (k \neq 0 ， x < 0)$ 上运动，则 $k =$ .

查看试题解析

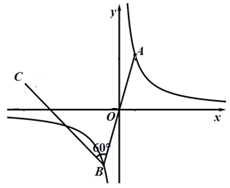
三、解答题

17. 计算： $| - \sqrt{8} | + {(π - 1)}^{0} + {(\frac{1}{2})}^{- 1}$

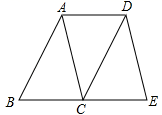
查看试题解析
18. 已知：如图，E是▱ABCD的边BC延长线上的一点，且CE＝BC．
求证：△ABC≌△DCE．

查看试题解析
19. 先化简，再求值： $(\frac{4}{m} + m - 4) \div \frac{m^{2} - 4}{2 + m}$ ，其中 $m = \sqrt{3}$ .

查看试题解析
20. 某茶农在科技特派员的指导下，进行“智慧茶山”的项目管理，因此茶叶品质和产量都在提升.现茶农有两种方式销售茶叶：一是直接销售刚采摘的茶青，二是制成精茶销售.若3kg茶青和2kg精茶可售660元；6kg茶青和1kg精茶可售420元.

(1)、求每千克茶青和每千克精茶的售价.

(2)、如果销售茶青和精茶共100千克，且总售价不超过8000元，那么至少要销售茶青多少千克？（结果保留整数）

查看试题解析
21. 某厂接受了一项加工业务，加工出来的产品（单位：件）按标准分为A，B，C，D四个等级.加工业务约定：对于A级品、B级品、C级品，厂家每件分别收取加工费90元，50元，20元；对于D级品，厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件，乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务，在两个分厂各试加工了100件这种产品，并统计了这些产品的等级，整理如下：
甲分厂产品等级的频数分布表

等级

A

B

C

D

频数

40

20

20

20

乙分厂产品等级的频数分布表

等级

A

B

C

D

频数

28

17

34

21

(1)、分别估计甲、乙两分厂加工出来的一件产品为A级品的概率；

(2)、分别求甲、乙两分厂加工出来的100件产品的平均利润，以平均利润为依据，厂家应选哪个分厂承接加工业务？

查看试题解析
22. 我们规定：在一个三角形中，如果一个内角的度数是另一个内角度数的3倍，那么这样的三角形称为“3倍角三角形”.如图， $△ A B C$ 为锐角三角形，AB＝AC，CD∥AB.

(1)、当∠BAC＝40°时，判断 $△ A B C$ 是否为“3倍角三角形”；

(2)、用直尺和圆规作出线段BP，使得点P在直线CD上，且∠ABP＝ $\frac{1}{2}$ ∠BAC，将AC与BP的交点记为点E，若 $△$ PEC为“3倍角三角形”，求∠BAC.

查看试题解析
23. 如图，在Rt△ABC中，∠ACB＝90°，以斜边AB上的中线CD为直径作O⊙，与BC交于点M，与AB的另一个交点为E，过M作MN⊥AB，垂足为N.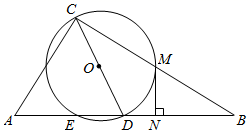

(1)、求证：MN是⊙O的切线；

(2)、若⊙O的直径为5，sinB＝ $\frac{3}{5}$ ，求ED的长.

查看试题解析
24. 如图，在矩形ABCD中，AB＝6，BC＝8，点E是AD边上的动点，将矩形ABCD沿BE折叠，点A落在点 $A^{'}$ 处，连接 $A^{'} C$ .

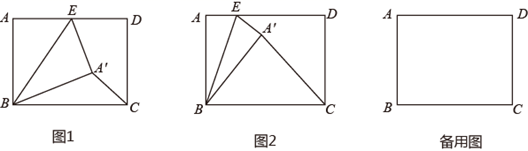(1)、如图1，求证：∠DE $A^{'}$ ＝2∠ABE；

(2)、如图2，若AE＝2，求 $S_{△ A^{'} C B}$ .

(3)、点E在AD边上运动的过程中，∠ $A^{'}$ CB的度数是否存在最大值，若存在，求出此时线段AE的长；若不存在，请说明理由.

查看试题解析
25. 将抛物线C：y＝（x﹣1）²向下平移4个单位长度得到抛物线C₁ ，再将抛物线C₁向左平移1个单位长度得到抛物线C₂.

(1)、直接写出抛物线C₁ ， C₂的解析式；

(2)、如图（1），抛物线C₁与 $x$ 轴交于A，B两点，与 $y$ 轴交于C点，且D为第四象限抛物线上一点，连接AD，BC交于点E，连接BD，记 $△$ BDE的面积为S₁ ， $△$ ABE的面积为S₂ ，求 $\frac{S_{1}}{S_{2}}$ 的最大值；

(3)、如图（2），直线y＝kx（k≠0，k为常数）与抛物线C₂交于E，F两点，M为线段EF的中点；直线 $y = - \frac{4}{k} x$ 与抛物线C₂交于G，H两点，N为线段GH的中点.求证：直线MN经过一个定点.

查看试题解析

等级	A	B	C	D
频数	40	20	20	20

等级	A	B	C	D
频数	28	17	34	21