河南省南阳市淅川县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-24 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{16}$ 的平方根是（　　）

A、±4 B、4 C、±2 D、2

查看试题解析
2. 下列运算正确的是（）.

A、 $x^{6} \cdot x^{2} = x^{12}$ B、 $x^{6} + x^{2} = x^{3}$ C、 ${(x^{6})}^{2} = x^{8}$ D、 ${(- x)}^{6} \div x^{2} = x^{4}$

查看试题解析
3. 下列多项式中，不能用完全平方公式分解因式的是（）

A、 $m + 1 + \frac{m^{2}}{4}$ B、 $- x^{2} + 2 x y - y^{2}$ C、 $- x^{2} + 14 x y + 49 y^{2}$ D、 $\frac{x^{2}}{9} - \frac{2}{3} x + 1$

查看试题解析
4. 下列命题是假命题的有（　　）.
①若a²＝b² ，则a＝b；②一个角的余角大于这个角；③若a，b是有理数，则|a＋b|＝|a|＋|b|；④如果∠A＝∠B，那∠A与∠B是对顶角.

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图所示的4×4正方形网格中，∠1+∠2+∠3+∠4+∠5+∠6+∠7=（）

A、330° B、315° C、310° D、320°

查看试题解析
6. 若 $5^{x} = 3$ ， $5^{y} = 2$ ，则 $5^{2 x - 3 y} =$ （）

A、 $\frac{3}{4}$ B、1 C、 $\frac{2}{3}$ D、 $\frac{9}{8}$

查看试题解析
7. 如果 $(x + m) (x + \frac{1}{5})$ 的结果不含x项，则m的值是（）

A、 $\frac{1}{5}$ B、5 C、 $- \frac{1}{5}$ D、 $- 5$

查看试题解析
8. 等式 $(- a - 1) \cdot () = a^{2} - 1$ 中，括号内应填入（）

A、 $a + 1$ B、 $1 - a$ C、 $- 1 - a$ D、 $a - 1$

查看试题解析
9. 如图，已知∠ABC＝∠BAD ，再添加一个条件，仍不能判定△ABC≌△BAD的是（　　）

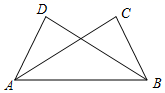A、AC＝BD B、∠C＝∠D C、AD＝BC D、∠ABD＝∠BAC

查看试题解析
10. 已知一个等腰三角形 $△ A B C$ 的两边长为5，7，另一个等腰三角形 $△ A B C$ 的两边为 $2 x - 3$ ， $3 x - 5$ ，若两个三角形全等，则x的值为（）

A、5 B、4 C、4或5 D、 $\frac{10}{3}$

查看试题解析

二、填空题

11. 请写出一个大于1且小于2的无理数：.

查看试题解析
12. 计算： ${(0.04)}^{99} \times {[{(- 5)}^{99}]}^{2}$ 的结果是.

查看试题解析
13. 如图，有一个池塘，要测池塘两端A，B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接达到点A和B，连接AC并延长到点D，使CD=CA，连接BC并延长到点E，使CE=CB，连接DE，那么量出DE的长度就是A，B的距离，这是根据全等三角形判定证明全等，从而得出 $D E$ 的长就是A，B的距离.

查看试题解析
14. 若 $4 x^{2} - m x y + 9 y^{2}$ 是一个完全平方式，则 $m =$

查看试题解析
15. 已知：如图，在长方形ABCD中，AB＝4，AD＝6.延长BC到点E，使CE＝2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为秒时，△ABP和△DCE全等.

查看试题解析

三、解答题

16. 计算

(1)、 $- \sqrt[3]{- \frac{1}{64}} - \sqrt{{(- 5)}^{2}} + \frac{1}{\sqrt{0.04}}$

(2)、 $2018^{2} - 2019 \times 2017$

查看试题解析
17. 计算： $2 x^{2} \cdot (\frac{1}{2} x y^{2} - y) - (x^{2} y^{2} - x y) \cdot (- 3 x)$

查看试题解析
18. 先化简，再求值.
$(2 + a) (2 - a) + a (a - 5 b) + 3 a^{5} b^{3} \div {(- a^{2} b)}^{2}$ ，其中 $a b = - \frac{1}{2}$

查看试题解析
19. 若x，y满足 $x^{2} + y^{2} = 8$ ， $x y = 2$ ，求下列各式的值.

(1)、 ${(x + y)}^{2}$

(2)、 $x - y$

(3)、 $x^{3} y + x y^{3}$

查看试题解析
20. 对于任意实数a、b、c、d，我们规定符号的意义是 $| \begin{matrix} a & b \\ c & d \end{matrix} | = a d - b c$ 按照这个规律计算：

(1)、 $| \begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix} | =$

(2)、当 $x^{2} - 3 x + 1 = 0$ 时，求 $| \begin{matrix} x + 1 & 3 x \\ x - 2 & x - 1 \end{matrix} |$ 的值.

查看试题解析
21. 如图，已知点B、E、C、F在一直线上， $A B = D F$ ， $A C = D E$ ， $∠ A = ∠ D$

(1)、求证： $A C // D E$ ；

(2)、若 $B F = 10$ ， $E C = 2$ ，求 $B C$ 的长.

查看试题解析
22. 老师在讲完乘法公式 ${(a \pm b)}^{2} = a^{2} \pm 2 a b + b^{2}$ 的多种运用后，要求同学们运用所学知识解答：求代数式 $x^{2} + 4 x + 5$ 的最小值？同学们经过交流、讨论，最后总结出如下解答方法：
解： $x^{2} + 4 x + 5 = x^{2} + 4 x + 4 + 1 = {(x + 2)}^{2} + 1$

∵ ${(x + 2)}^{2} \geq 0$

即当 $x = - 2$ 时， ${(x + 2)}^{2}$ 的值最小，最小值是0，

∴ ${(x + 2)}^{2} + 1 \geq 1$

当 ${(x + 2)}^{2} = 0$ 时， ${(x + 2)}^{2} + 1$ 的值最小，最小值是1，

∴ $x^{2} + 4 x + 5$ 的最小值是1.

请你根据上述方法，解答下列各题

(1)、当 $x =$ 时，代数式 $x^{2} - 6 x + 12$ 的最小值是；

(2)、若 $y = - x^{2} + 2 x - 3$ ，当 $x =$ 时， $y$ 有最值（填“大”或“小”），这个值是；

(3)、若 $y = x^{2} - 3 x - 5$ ，求 $y + x$ 的最小值.

查看试题解析
23. 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．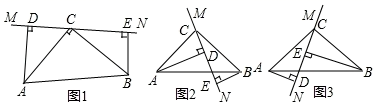

(1)、当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；

(2)、当直线MN绕点C旋转到图2的位置时，求证：DE=AD﹣BE；

(3)、当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．

查看试题解析