河南省漯河市郾城区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-09-24 类型:期中考试
一、单选题
-
1. 在下列与食品标志有关的图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形3. 下列选项中的三条线段中,能构成三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 已知△ABC≌△A′B′C′,若∠A=50°,∠B′=80°,则∠C的度数是( )A、30° B、40° C、50° D、60°5. 如图所示,下面甲、乙、丙三个三角形和 全等的图形是( )
2. 在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形3. 下列选项中的三条线段中,能构成三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 已知△ABC≌△A′B′C′,若∠A=50°,∠B′=80°,则∠C的度数是( )A、30° B、40° C、50° D、60°5. 如图所示,下面甲、乙、丙三个三角形和 全等的图形是( )
 A、甲和乙 B、乙和丙 C、只有丙 D、只有乙6. 到△ABC的三个顶点距离相等的点是△ABC的( )A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边垂直平分线的交点7. 如图, 与 关于直线l对称,下列判断错误的是( )
A、甲和乙 B、乙和丙 C、只有丙 D、只有乙6. 到△ABC的三个顶点距离相等的点是△ABC的( )A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边垂直平分线的交点7. 如图, 与 关于直线l对称,下列判断错误的是( )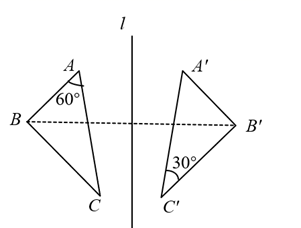 A、 B、直线l垂直平分线段 C、 D、8. 如图所示,在 中, ,点D在 上, , 交 于点E, 的周长为12, 的周长为6,则 长为( )
A、 B、直线l垂直平分线段 C、 D、8. 如图所示,在 中, ,点D在 上, , 交 于点E, 的周长为12, 的周长为6,则 长为( ) A、3 B、4 C、5 D、69. 如图, 的面积为 , 垂直 的平分线 于P,则 的面积为( )
A、3 B、4 C、5 D、69. 如图, 的面积为 , 垂直 的平分线 于P,则 的面积为( ) A、 B、 C、 D、10. 如图,C为线段 上一动点(不与点A,E重合),在 同侧分别作正三角形 和正三角形 , 与 交于点O, 与 交于点G, 与 交于点F.以下几个结论:
A、 B、 C、 D、10. 如图,C为线段 上一动点(不与点A,E重合),在 同侧分别作正三角形 和正三角形 , 与 交于点O, 与 交于点G, 与 交于点F.以下几个结论:① ;② ;③ ;④ ,⑤ ,恒成立的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 点 关于 轴对称的点的坐标为 .12. 等腰三角形周长是29,其中一边长是7,则等腰三角形的底边长是.13. 如图,在 中, , 和 的平分线交于点E,则 的度数是.
 14. 如图, 是等边三角形, 是 边上的高,E是 的中点,P是 上的一个动点,当 与 的和最小时,则 的度数是.
14. 如图, 是等边三角形, 是 边上的高,E是 的中点,P是 上的一个动点,当 与 的和最小时,则 的度数是.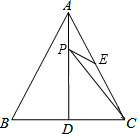 15. 如图, 中, , , , ,点P与点Q分别在线段 和 的垂线 上移动,则当 时, 与 全等.
15. 如图, 中, , , , ,点P与点Q分别在线段 和 的垂线 上移动,则当 时, 与 全等.
三、解答题
-
16. 已知一个多边形的内角和比它的外角和的3倍还多180度.(1)、求这个多边形的边数;(2)、求这个多边形的对角线的总条数.17. 如图, 中, , 是 上的高, 平分 .
 (1)、若 , ,求 与 的度数.(2)、聪明的你再取两组 和 的度数,算一算,想一想,请直接写出求 、 、 之间的关系,你的结论是.(不必写出证明过程)18. 已知,如图, 是 的一个外角, .
(1)、若 , ,求 与 的度数.(2)、聪明的你再取两组 和 的度数,算一算,想一想,请直接写出求 、 、 之间的关系,你的结论是.(不必写出证明过程)18. 已知,如图, 是 的一个外角, .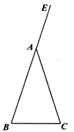 (1)、利用尺规作出 的角平分线 ;(不写作法,保留作图痕迹)(2)、判断 与 的位置关系,并写出证明过程.19. 如图,点A、F、C、D四点在一条直线上, , .
(1)、利用尺规作出 的角平分线 ;(不写作法,保留作图痕迹)(2)、判断 与 的位置关系,并写出证明过程.19. 如图,点A、F、C、D四点在一条直线上, , .老师说:再添加一个条件就可以使 .下面是课堂上三个同学的发言,甲说:添加 ;乙说:添加 ;丙说:添加 .
 (1)、甲、乙、丙三个同学说法正确的是.(2)、请你从正确的说法中选择一种,写出已知,求证和证明过程.20. 如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q.
(1)、甲、乙、丙三个同学说法正确的是.(2)、请你从正确的说法中选择一种,写出已知,求证和证明过程.20. 如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q. (1)、求∠BPQ的度数;(2)、若PQ=3,EP=1,求AD的长.21. 填空,完成下列证明过程
(1)、求∠BPQ的度数;(2)、若PQ=3,EP=1,求AD的长.21. 填空,完成下列证明过程已知,如图, 中, 平分 , 且平分 , 于E, 于F.求证: .
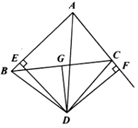
证明: 且平分 ,
( ).
为 的平分线, , ,
_▲_=_▲_(角的平分线上的点到角的两边的距离相等),
.
在 和 中,
, ,
_▲_( ),
( ).
在 和 中,
,▲_=_▲_,
,
_▲_ .
_▲_ .
22. 已知, 是等边三角形,点E在边 上,点D在边 的延长线上,且 . (1)、如图1,当点E为 中点时,则线段 与 的大小关系是;(2)、如图2,当点E为 边上任一点时,(1)中的结论是否还成立?若成立,请写出证明过程;若不成立,说明理由.23. 如图,平面直角坐标系中有点B(﹣1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
(1)、如图1,当点E为 中点时,则线段 与 的大小关系是;(2)、如图2,当点E为 边上任一点时,(1)中的结论是否还成立?若成立,请写出证明过程;若不成立,说明理由.23. 如图,平面直角坐标系中有点B(﹣1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d). (1)、当a=2时,则C点的坐标为( , );(2)、动点A在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.(3)、当a=2时,在坐标平面内是否存在一点P(不与点C重合),使△PAB与△ABC全等?若存在,直接写出P点坐标;若不存在,请说明理由.
(1)、当a=2时,则C点的坐标为( , );(2)、动点A在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.(3)、当a=2时,在坐标平面内是否存在一点P(不与点C重合),使△PAB与△ABC全等?若存在,直接写出P点坐标;若不存在,请说明理由.