河南省洛阳市汝阳县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-24 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列各数中是无理数的有（）
$- 0.111 \dots$ ， $\sqrt{4}$ ， $\sqrt{5}$ ， $3 π$ ， $3.1415926$ ， $2.010101 \dots$ （相邻两个0之间有1个1）， $76.01020304050607 \dots$ ， $\sqrt[3]{2}$ .

A、3个 B、4个 C、5个 D、6个

查看试题解析
2. 下列运算正确的是（）

A、 $a^{3} \cdot a^{3} = a^{9}$ B、 ${(a^{3})}^{2} = a^{5}$ C、 $a^{2} + a^{3} = 2 a^{5}$ D、 ${(- a^{2})}^{3} = - a^{6}$

查看试题解析
3. 计算 $6 m^{6} \div {(- 2 m^{2})}^{3}$ 的结果为（）

A、 $- m$ B、 $- 1$ C、 $\frac{3}{4}$ D、 $- \frac{3}{4}$

查看试题解析
4. 下列等式从左到右的变形，属于因式分解的是（　　）

A、 $x^{2} + 2 x - 1 = {(x - 1)}^{2}$ B、 $(a + b) (a - b) = a^{2} - b^{2}$ C、 $x^{2} + 4 x + 4 = {(x + 2)}^{2}$ D、 $a x^{2} - a = a (x^{2} - 1)$

查看试题解析
5. 等腰三角形两条边长分别为12、15，则这个三角形的周长为（　　）

A、27 B、39 C、42 D、39或42

查看试题解析
6. 如图，在 $Δ A B D$ 和 $Δ A C E$ 中， $A B = A C$ ，则下列补充条件中不能说明 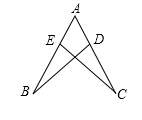$Δ A B D ≅ Δ A C E$ 的是（）

A、 $A D = A E$ B、 $C E = B D$ C、 $∠ C = ∠ B$ D、 $∠ A D B = ∠ A E C$

查看试题解析
7. 已知两个直角三角形全等，其中一个直角三角形的面积为3，斜边为4，则另一个直角三角形斜边上的高为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{4}$ C、 $\frac{3}{2}$ D、 $6$

查看试题解析
8. 如图，边长为(m+5)的正方形纸片剪出一个边长为m的正方形之后，剩余部分可剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为5，则另一边长是（）

A、m+3 B、m+5 C、2m+5 D、2m+10

查看试题解析
9. 如图所示，把 $△ A B C$ 绕C点旋转 $35 °$ ，得到 $△ A^{'} B^{'} C^{'}$ ， $A^{'} B^{'}$ 交 $A C$ 于点D，若 $∠ A^{'} D C = 90 °$ ，则 $∠ A$ 等于（）

A、 $35 °$ B、 $65 °$ C、 $55 °$ D、 $45 °$

查看试题解析
10. 如图1，已知 $A B = A C$ ，D为 $∠ B A C$ 的角平分线上面一点，连接 $B D$ ， $C D$ ；如图2，已知 $A B = A C$ ， $D$ 、 $E$ 为 $∠ B A C$ 的角平分线上面两点，连接 $B D$ ， $C D$ ， $B E$ ， $C E$ ；如图3，已知 $A B = A C$ ，D、E、F为 $∠ B A C$ 的角平分线上面三点，连接 $B D$ ， $C D$ ， $B E$ ， $C E$ ， $B F$ ， $C F$ ；…，依次规律，第n个图形中有全等三角形的对数是（）.

A、 $n$ B、 $2 n - 1$ C、 $\frac{n (n + 1)}{2}$ D、 $3 (n + 1)$

查看试题解析

二、填空题

11. $\frac{1}{2}$ 是的平方根.

查看试题解析
12. 命题“根据客观事实能够判断一件事情真假的语句，叫做命题.”是命题（填“真”或“假”）.

查看试题解析
13. 阅读理解：引入新数 $i$ ，新数 $i$ 满足分配律，结合律，交换律.已知 $i^{2} = - 1$ ，那么 $(1 + i) \cdot (1 - i) =$ .

查看试题解析
14. $| - 5 | + {(- 2)}^{2} + \sqrt[3]{- 27} - \sqrt{{(- 2)}^{2}} =$ .

查看试题解析
15. 中国古代称直角三角形为勾股形，其中直角边中较小者为勾，另一长直角边为股，斜边为弦，有一个基本的几何定理，称之为勾股定理.它指直角三角形的两条直角边长（古称勾长、股长）的平方和等于斜边长（古称弦长）的平方.如果设直角三角形的两条直角边长度分别是a和b，斜边长度是c，那么可以用数学语言表达 $a^{2} + b^{2} = c^{2}$ ，这是一个基本事实.利用这个基本事实解决下列问题.
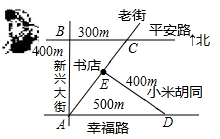
如图，平安路与幸福路是两条平行的道路，且与新兴大街垂直，老街与小米胡同垂直，书店位于老街与小米胡同的交口处，如果小强同学站在平安路与新兴大街的交叉路口，准备去书店，按图中的街道行走，最近的路程为m.

查看试题解析

三、解答题

16. 计算： $\frac{4}{3} a^{6} b^{8} \div {(- \frac{1}{3} a b^{2})}^{2} - \frac{1}{2} a^{2} \cdot {(- 6 a b^{2})}^{2}$

查看试题解析
17. 先化简再求值 $(2 x + 3) (2 x - 3) - 4 x (x - 1) + {(x - 2)}^{2}$ ，其中 $x = - 1$ .

查看试题解析
18. 用简便方法计算（结果用科学记数法表示）

(1)、 ${0.25}^{9} \times 2^{20} \times 25^{9} \times 64^{3}$ ：

(2)、 $2001^{2} - 4002 + 1$ .

查看试题解析
19. 观察“探究性学习”小组的甲、乙两名同学进行的分解因式：
甲： $x^{2} - x y + 4 x - 4 y$         乙： $a^{2} - b^{2} - c^{2} + 2 b c$

$= (x^{2} - x y) + (4 x - 4 y)$ （分成两组）    $= a^{2} - (b^{2} + c^{2} - 2 b c)$ （分成两组）

$= x (x - y) + 4 (x - y)$ （直接提公因式）    $= a^{2} - {(b - c)}^{2}$ （直接运用公式）

$= (x - y) (x + 4)$ .        $= (a + b - c) (a - b + c)$ （再用平方差公式）

请你在他们解法的启发下，把下列各式分解因式：

(1)、 $m^{3} - 2 m^{2} - 4 m + 8$ ；

(2)、 $x^{2} - 2 x y - 9 + y^{2}$ .

查看试题解析
20. 现有两张铁皮，长方形铁皮的长为x+2y，宽为x-2y（x-2y>0）；正方形铁皮的边长为2(x-y).现根据需要，要把两张铁皮焊接成一张长方形的铁皮，新铁皮长6x，请你求出新铁皮的宽.

查看试题解析
21. 如图，点P是等边 $Δ X Y Z$ 内的一点，连接 $P X$ 、 $P Y$ 、 $P Z$ ，以 $Y P$ 为一边作 $∠ P Y Q = 60 °$ ，且 $Y Q = Y P$ ，连接 $Z Q$ .试观察猜想 $X P$ 与 $Z Q$ 的大小关系，并加以证明.

查看试题解析
22. 如图， $A B = C B$ ， $∠ A B C = 90 °$ ，D为 $A B$ 延长线上一点，点E在 $B C$ 边上，且 $B E = B D$ ，连结 $A E$ 、 $D E$ 、 $D C$ .

(1)、求证： $Δ A B E ≅ Δ C B D$ ；

(2)、若 $A B = 6$ ， $C E = 2 B E$ ，求 $Δ A D C$ 的面积.

查看试题解析
23. 如图1， $Δ A B C$ 的边 $B C$ 在直线 $l$ 上， $A C ⊥ B C$ ，且 $A C = B C$ ； $Δ E F P$ 的边 $F P$ 也在直线 $l$ 上，边 $E F$ 与边 $A C$ 重合，且 $E F = F P$ .

(1)、示例：在图1中，通过观察、测量，猜想并写出 $A B$ 与 $A P$ 所满足的数量关系和位置关系.
答： $A B$ 与 $A P$ 的数量关系和位置关系分别是、.

(2)、将 $Δ E F P$ 沿直线 $l$ 向左平移到图2的位置时， $E P$ 交 $A C$ 于点Q， $C Q = C P$ ，连结 $A P$ ， $B Q$ .请你观察、测量，猜想并写出 $B Q$ 与 $A P$ 所满足的数量关系和位置关系.
答： $B Q$ 与 $A P$ 的数量关系和位置关系分别是、.

(3)、将 $Δ E F P$ 沿直线 $l$ 向左平移到图3的位置时， $E P$ 的延长线交 $A C$ 的延长线于点Q， $C Q = C P$ ，连结 $A P$ 、 $B Q$ .你认为（2）中所猜想的 $B Q$ 与 $A P$ 的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由.

查看试题解析