湖北省十堰市房县2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2021-09-24 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，最小的数是（）

A、－3 B、0 C、1 D、2

查看试题解析
2. 某厂家生产一种袋装食品的标准重量是500克，质检员把每袋超出的部分记作正数，不足的部分记作负数，质检员随机测得一袋食品质量为501克，则记作（）

A、﹣1 B、1 C、0 D、501

查看试题解析
3. 数轴上的点A表示的数是a，当点A在数轴上向右平移了6个单位长度后得到点B，若点A和点B表示的数恰好互为相反数，则数a是（）

A、6 B、﹣6 C、3 D、﹣3

查看试题解析
4. 下列说法正确的是（）

A、近似数0.21与0.210的精确度相同 B、近似数1.3×10⁴精确到十分位 C、1 189 000这个数用科学记数法可表示为1.189×10⁶ D、小明的身高为161 cm中的数是准确数

查看试题解析
5. 若数a，b在数轴上的位置如图示，则（）

A、a+b＞0 B、ab＞0 C、a﹣b＞0 D、﹣a﹣b＞0

查看试题解析
6. 下列式子中是单项式的个数为（）
① $- \frac{1}{3} x^{5} y^{2}$ ，② $\frac{3 y^{2}}{x}$ ，③ $0$ ，④ $\frac{2}{3} x^{2} y^{7}$ ，⑤ $- \frac{x}{7}$ ，⑥ $2 x^{2} - 1$ ，⑦ $- \frac{5 x^{2} y^{4}}{6}$ ，⑧ $- 1.96$ ，

⑨ $m - 2$ ，⑩ $- \frac{m n}{2}$

A、5个 B、6个 C、7个 D、8个

查看试题解析
7. 下列运算中，“去括号”正确的是（　　）

A、a＋（b－c）=a－b－c B、a－（b＋c）=a－b－c C、m－2（p－q）=m－2p＋q D、x²－（－x＋y）=x²＋x＋y

查看试题解析
8. 下列计算中结果正确的是（）

A、4+5ab=9ab B、6xy﹣x=6y C、3a²b﹣3ba²=0 D、12x³+5x⁴=17x⁷

查看试题解析
9. 一个两位数，十位上的数字为a，个位上的数字比十位上的数字少2，则这个两位数为（）

A、11a－20 B、11a+20 C、11a－2 D、11a+2

查看试题解析
10.
下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有3颗棋子，第②个图形一共有9颗棋子，第③个图形一共有18颗棋子，…，则第⑧个图形中棋子的颗数为（）

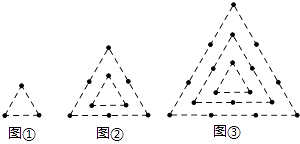A、84 B、108 C、135 D、152

查看试题解析

二、填空题

11. 已知： $| a | = 3$ ， $b^{2} = 4$ ， $a b < 0$ ，a-b的值为.

查看试题解析
12. 如果单项式3x^my与﹣5x³yⁿ是同类项，那么m+n＝．

查看试题解析
13. 根据如右图所示的程序计算，若输入x的值为1，则输出y的值为.

查看试题解析
14. 已知2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，…，则2²⁰²⁰的个位数字是.

查看试题解析

三、解答题

15. 计算：(﹣5)+(+7)﹣(﹣3)﹣(+20)

查看试题解析
16. 计算：25 $\div \frac{5}{6} \times (- \frac{2}{5})+(-2) \times {(-1)}^{2019}$

查看试题解析
17. 化简并求值：(3a²﹣7bc﹣6b²)﹣(5a²﹣3bc+4b²)其中，a＝2，b＝﹣1，c= $\frac{5}{2}$ .

查看试题解析
18. 化简并求值：5x²﹣[x²﹣2x﹣2（x²﹣3x+1）]其中，3x²＝2x+5.

查看试题解析
19. 我们规定“※”是一种数学运算符号，两数 $A$ 、 $B$ 通过“※”运算是 $(A + 2) \times 2 - B$ ，即 $A$ ※ $B$ $= (A + 2) \times 2 - B$ ，
例如： $3$ ※ $5$ $= (3 + 2) \times 2 - 5 = 5$

(1)、求：7※9的值；

(2)、求：（7※9）※（-2）的值.

查看试题解析
20. 观察下面三行数：
－3，9，－27，81，-243 ， …；①

-5，7，-29， 79，-245，…；②

－1，3，－9，27，-81，….③

(1)、第①行数第2020个数为；

(2)、第②行第n个数为第③行第n个数为；

(3)、分别写出第①②③行的第10个数，并求出它们的和.

查看试题解析
21. 某公司6天内货品进出仓库的吨数如下，其中正数表示进库的吨数：
+31，-32，-16，+35，-38，-20．

(1)、经过这6天，仓库里的货品是（填“增多了”或“减少了”）．

(2)、经过这6天，仓库管理员结算发现仓库里还有货品460吨，那么6天前仓库里有货品多少吨？

(3)、如果进出的装卸费都是每吨5元，那么这6天要付多少元装卸费？

查看试题解析
22. 如图所示，是两种长方形铝合金窗框，已知窗框的长都是y米，宽都是x米，已知一用户需A型的窗框2个，B型的窗框3个.

(1)、用含x、y的式子表示共需铝合金的长度（窗框本身宽度忽略不计）；

(2)、若1米铝合金的平均费用为100元，求当x＝1.5，y＝2.5时，（1）中铝合金的总费用为多少元？

查看试题解析
23. 某超市在春节期间对顾客实行优惠，规定如下：
一次性购物
优惠办法
少于200元
不予优惠
低于500元但不低于200元
九折优惠
500元或超过500元
其中500元部分给予九折优惠，超过500元部分给予八折优惠

(1)、王老师一次性购物600元，他实际付款元．

(2)、若顾客在该超市一次性购物x元，当x小于500元但不小于200时，他实际付款元，当x大于或等于500元时，他实际付款元．（用含x的代数式表示）．

(3)、如果王老师两次购物货款合计820元，第一次购物的货款为a元（200＜a＜300），用含a的代数式表示：两次购物王老师实际付款多少元？

查看试题解析
24. 如图，数轴上有A，B，C三点，它们分别表示数a，b，c，已知|a＋24|＋(b+10)²＝0，且b，c互为相反数.

(1)、求a，b，c的值；

(2)、若有两只电子蚂蚁甲、乙分别从A，C两点同时出发相向而行，电子蚂蚁甲的速度为4个单位长度/秒，电子蚂蚁乙的速度为6个单位长度/秒，当两只蚂蚁在数轴上点m处相遇时，求点m表示的数；

(3)、若电子蚂蚁丙从A点出发以4个单位长度/秒的速度向右爬行，多少秒后电子蚂蚁丙到A，B，C的距离和为40个单位长度？

查看试题解析

一次性购物	优惠办法
少于200元	不予优惠
低于500元但不低于200元	九折优惠
500元或超过500元	其中500元部分给予九折优惠，超过500元部分给予八折优惠