江苏省无锡市江阴市澄西片2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-24 类型:期中考试
一、单选题
-
1. 下列轴对称图形中,对称轴条数最多的是( )A、线段 B、等边三角形 C、正方形 D、圆2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 关于 的方程 有两个相等的实数根,则 的值是( )A、 B、 C、 D、4. 如图, 中, , , ,则 的长是( )
 A、 B、 C、 D、5. 如图,在 外任取一点 ,连接 , , ,并取它们的中点 , , ,连接 , , ,得 ,则下列说法错误的是( )
A、 B、 C、 D、5. 如图,在 外任取一点 ,连接 , , ,并取它们的中点 , , ,连接 , , ,得 ,则下列说法错误的是( ) A、 与 是位似图形 B、 与 是相似图形 C、 与 的周长比为 D、 与 的面积比为6. 如图,点 , , , 在射线 上,点 , , 在射线 上,且 , .若 , 的面积分别为 ,8,则图中三个阴影三角形面积之和为( )
A、 与 是位似图形 B、 与 是相似图形 C、 与 的周长比为 D、 与 的面积比为6. 如图,点 , , , 在射线 上,点 , , 在射线 上,且 , .若 , 的面积分别为 ,8,则图中三个阴影三角形面积之和为( ) A、 B、 C、 D、7. 如图2,在平面直角坐标系中,点 的坐标为(1,4)、(5,4)、(1、 ),则 外接圆的圆心坐标是
A、 B、 C、 D、7. 如图2,在平面直角坐标系中,点 的坐标为(1,4)、(5,4)、(1、 ),则 外接圆的圆心坐标是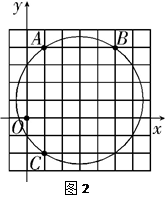 A、(2,3) B、(3,2) C、(1,3) D、(3,1)8. 太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是10cm,则皮球的直径是( )
A、(2,3) B、(3,2) C、(1,3) D、(3,1)8. 太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是10cm,则皮球的直径是( ) A、5 B、15 C、10 D、89. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm10. 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在AD,BC上,连结OG,DG,若OG⊥DG,且☉O的半径长为1,则下列结论不成立的是( )
A、5 B、15 C、10 D、89. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm10. 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在AD,BC上,连结OG,DG,若OG⊥DG,且☉O的半径长为1,则下列结论不成立的是( )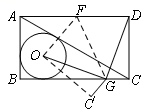 A、CD+DF=4 B、CD−DF=2 −3 C、BC+AB=2 +4 D、BC−AB=2
A、CD+DF=4 B、CD−DF=2 −3 C、BC+AB=2 +4 D、BC−AB=2二、填空题
-
11. 在比例尺为 的某省地图上,量得 地到 地的距离约为 厘米,则 地到 地的实际距离约为千米.12. 已知 ,则 .13. 方程2x-4=0的解也是关于x的方程x2+mx+2=0的一个解,则m的值为 .
14. 若关于 的方程 的两根均是整数,则 的值可以是.(只要求写出两个)15. 在平行四边形 中, 为靠近点 的 的三等分点,连结 ,交 于点 , ,则 为. 16. 如图,在直角三角尺 中, ,把直角三角尺 放置在圆上, 经过圆心 , 与 相交于 , 两点,点 , , 的刻度分别是 , , , 与 相切于 点,那么 的半径是 .
16. 如图,在直角三角尺 中, ,把直角三角尺 放置在圆上, 经过圆心 , 与 相交于 , 两点,点 , , 的刻度分别是 , , , 与 相切于 点,那么 的半径是 . 17. 有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是cm2 . (结果保留π)18. 如图,在 中, , , ,经过点 且与边 相切的动圆与 , 分别相交于点 , ,则线段 长度的最小值是.
17. 有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是cm2 . (结果保留π)18. 如图,在 中, , , ,经过点 且与边 相切的动圆与 , 分别相交于点 , ,则线段 长度的最小值是.
三、解答题
-
19.(1)、 ;(2)、 ;(3)、 .20. 已知关于x的方程 x2-5x-m2-2m-7=0.(1)、若此方程的一个根为-1,求m的值;(2)、求证:无论m取何实数,此方程都有两个不相等的实数根.21. 如图,在矩形ABCD中,AB=2,BC=3,M是BC的中点,DE⊥AM于点E.
 (1)、求证:△ADE∽△MAB;(2)、求DE的长.22. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ落在地面上的影子PM=1.8m,落在墙上的影子MN=1.1m,求木竿PQ的长度.
(1)、求证:△ADE∽△MAB;(2)、求DE的长.22. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ落在地面上的影子PM=1.8m,落在墙上的影子MN=1.1m,求木竿PQ的长度. 23. 如图,AB为⊙O的直径,C为⊙O上一点,AD与过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
23. 如图,AB为⊙O的直径,C为⊙O上一点,AD与过C点的直线互相垂直,垂足为D,且AC平分∠DAB. (1)、求证:DC为⊙O的切线;(2)、若⊙O的半径为3,AD=4,求AC的长.24. 如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)、求证:DC为⊙O的切线;(2)、若⊙O的半径为3,AD=4,求AC的长.24. 如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°. (1)、求证:DP是⊙O的切线;(2)、若⊙O的半径为3cm,求图中阴影部分的面积.25. 如图
(1)、求证:DP是⊙O的切线;(2)、若⊙O的半径为3cm,求图中阴影部分的面积.25. 如图 (1)、如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值 叫做AE与AB的黄金比.)(2)、如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(1)、如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值 叫做AE与AB的黄金比.)(2)、如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)
26. 今年深圳“读书月”期间,某书店将每本成本为30元的一批图书,以40元的单价出售时,每天的销售量是300本.已知在每本涨价幅度不超过10元的情况下,若每本涨价1元,则每天就会少售出10本,设每本书上涨了x元.请解答以下问题:(1)、填空:每天可售出书本(用含x的代数式表示);(2)、若书店想通过售出这批图书每天获得3750元的利润,应涨价多少元?27. 在 中, , , ,点 ,点 同时从点 出发,点 沿边 以 的速度向点 运动,点 从点 出发,沿边 以 的速度向点 运动(点 不与 , 重合,点 不与 , 重合),设运动时间为 .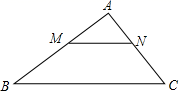 (1)、求证: ;(2)、当 为何值时,以 为直径的 与直线 相切?(3)、把 沿直线 折叠得到 ,若 与梯形 重叠部分的面积为 ,试求 关于 的函数表达式,并求 为何值时, 的值最大,最大值是多少?28. 小明热爱数学,在课外书上看到了一个有趣的定理——“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1, 在 中,点 为 的中点,根据“中线长定理”,可得: .小明尝试对它进行证明,部分过程如下:
(1)、求证: ;(2)、当 为何值时,以 为直径的 与直线 相切?(3)、把 沿直线 折叠得到 ,若 与梯形 重叠部分的面积为 ,试求 关于 的函数表达式,并求 为何值时, 的值最大,最大值是多少?28. 小明热爱数学,在课外书上看到了一个有趣的定理——“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1, 在 中,点 为 的中点,根据“中线长定理”,可得: .小明尝试对它进行证明,部分过程如下:解:过点 作 于点 ,如图2,在 中, ,
同理可得: , ,
为证明的方便,不妨设 , ,
…
 (1)、阅读理解:请你完成小明剩余的证明过程;(2)、理解运用:
(1)、阅读理解:请你完成小明剩余的证明过程;(2)、理解运用:①在 中,点 为 的中点, , , ,则 ;
②如图3, 的半径为 ,点 在圆内,且 ,点 和点 在 上,且 ,点 、 分别为 、 的中点,则 的长为;
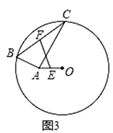 (3)、拓展延伸:小明解决上述问题后,联想到《能力训练》上的题目:如图 4,已知 的半径为 ,以 为直角顶点的 的另两个顶点 , 都在 上, 为 的中点,求 长的最大值.请你利用上面的方法和结论,求出 长的最大值.
(3)、拓展延伸:小明解决上述问题后,联想到《能力训练》上的题目:如图 4,已知 的半径为 ,以 为直角顶点的 的另两个顶点 , 都在 上, 为 的中点,求 长的最大值.请你利用上面的方法和结论,求出 长的最大值.