江苏省苏州市相城区2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-24 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程 $2 x^{2} + x - 3 = 0$ 的二次项系数是（）

A、2 B、1 C、 $- 3$ D、0

查看试题解析
2. 已知 $\frac{x}{y} = \frac{3}{5}$ ，则 $\frac{2 y}{x + y}$ 的值是（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{5}{4}$

查看试题解析
3. 如图，点A，B，C在⊙O上，D是 $\overset{⌢}{A B}$ 的中点，若 $∠ A O B = 100 °$ ，则 $∠ B C D$ 的度数是（）

A、20° B、25° C、30° D、35°

查看试题解析
4. 若 $△ A B C ∽ △ D E F$ 且周长之比1：3，则 $△ A B C$ 与 $△ D E F$ 的面积比是（）

A、1：3 B、 $1 ： \sqrt{3}$ C、1：9 D、3：1

查看试题解析
5. 已知关于x的一元二次方程 $x^{2} + b x - 1 = 0$ 有一个根为 $1 - \sqrt{2}$ ，则另一个根是（）

A、 $1 - \sqrt{2}$ B、 $1 + \sqrt{2}$ C、 $- 1 - \sqrt{2}$ D、 $- 1 + \sqrt{2}$

查看试题解析
6. 如图，在矩形ABCD中，点E是边AD上一点，且 $A E = 2 E D$ ，EC交对角线BD于点F，则 $\frac{E F}{F C}$ 等于（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
7. 一个两位数的两个数字的和为9，把这个两位数的个位数字与十位数字互换得到一个新的两位数，它与原两位数的积为1458，设原两位数的个位数字为x，则可列方程（）

A、 $[(9 - x) + x] [10 x + (9 - x)] = 1458$ B、 $[(9 - x) + x] [x + (9 - x)] = 1458$ C、 $[10 (9 - x) + x] [10 x + (9 - x)] = 1458$ D、 $[10 (9 - x) + x] [x + (9 - x)] = 1458$

查看试题解析
8. 正三角形内切圆与外接圆的半径的比值是（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
9. 定义运算： $a * b = a (1 - b)$ .若a，b是方程 $x^{2} - x + 2 m = 0 (m < 0)$ 的两根，则 $b * b - a * a$ 的值是（）

A、0 B、 $- 1$ C、2 D、2m

查看试题解析
10. 如图，⊙O的半径为3， $△ A B C$ 是⊙O的内接三角形，过点A作AD垂直BC于点D.若 $A D = 3$ ， $A C = 5$ ，则 $A B$ 长是（）

A、 $\frac{15}{4}$ B、4 C、 $\sqrt{13}$ D、 $\frac{18}{5}$

查看试题解析

二、填空题

11. $x^{2} + 6 x + 9 =$ （x+ ）²

查看试题解析
12. 在比例尺为1：100000的地图上，测量得到甲乙两座城市的距离为27cm，则甲乙两座城市的实际距离为千米.

查看试题解析
13. 如图，在半径为4的⊙O中， $\overset{⌢}{A B}$ 的长为 $π$ ，则阴影部分的面积为.

查看试题解析
14. 关于x的一元二次方程 $x^{2} - 2 x + k - 1 = 0$ 有两个不相等的实数根，则k的取值范围是.

查看试题解析
15. 将一个面积为 $6 π$ 的半圆围成一个圆锥，则该圆锥的底面半径为.

查看试题解析
16. 如图，在矩形ABCD中， $A B = 6 cm$ ， $B C = \sqrt{3} cm$ ，点P从点A出发沿AB以 $2 cm / s$ 的速度向点B移动，若出发t秒后， $P A = 2 P C$ ，则 $t =$ 秒.

查看试题解析
17. 如图，小明站在距地面5.1m的路灯OP下点A处，此时他的影长 $A E = 1 m$ ，小明沿直线向前走了2m到达了点B处，此时他的影长 $B F = 2 m$ ，则小明的身高为m.

查看试题解析
18. 已知线段 $A B = 4$ ，C是平面内任意一点，若 $∠ A C B = 45 °$ ，则 $△ A B C$ 面积的最大值是.

查看试题解析

三、解答题

19. 解方程：

(1)、 $4 x^{2} - 1 = 0$

(2)、 $3 x (x - 2) = (x - 2)$

(3)、 $x^{2} - 3 x + 2 = 0$

(4)、 ${(x + 3)}^{2} = 5 + 2 x$

查看试题解析
20. 如图，在 $△ A B C$ 中， $C H ⊥ A B$ 垂足为 $H$ ，且 $A C^{2} = A H \cdot A B$ .求证： $∠ A C B = 90 °$ .

查看试题解析
21. 已知如图，AB是⊙O的直径，C、D是圆上的两点，且 $∠ C D B = 2 ∠ C B D$ ，若 $∠ D B A = 30 °$ ，求 $∠ A D C$ 的度数.

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} - (2 m + 1) x + m - 2 = 0$ .

(1)、求证：不论m取何值，方程总有两个不相等的实数根；

(2)、若方程有两个实数根为 $x_{1}$ ， $x_{2}$ ，且 $x_{1} + x_{2} + 3 x_{1} x_{2} = 1$ ，求m的值.

查看试题解析
23. 如图在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (- 3 ， 2)$ ， $B (- 1 ， 3)$ ， $C (- 1 ， 1)$ ，请按如下要求画图：

(1)、以坐标原点O为旋转中心，将 $△ A B C$ 按顺时针方向旋转90°，得到 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ ，在旋转过程中点B所经过的路径长为 ▲ ；

(2)、以坐标原点O为位似中心，在x轴下方画出 $△ A B C$ 的位似图形 $△ A_{2} B_{2} C_{2}$ ，使它与 $△ A B C$ 的相似比为2：1

查看试题解析
24. 如图，在矩形 $A B C D$ 中，E是 $B C$ 的中点， $D F ⊥ A E$ ，垂足为F.

(1)、求证： $Δ A B E ∽ Δ D F A$ ；

(2)、若 $A B = 6$ ， $B C = 4$ ，求 $D F$ 的长.

查看试题解析
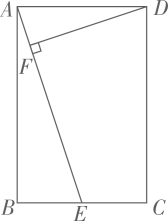25. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，以AC为直径作⊙O交AB于点D，E是BC的中点，连接DE并延长交AC的延长线于点F.

(1)、求证：DE是⊙O的切线；

(2)、若 $C E = 2$ ， $C F = 4$ ，求⊙O半径的长.

查看试题解析
26. 某水果超市以每千克20元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于40元，经市场调查发现，樱桃的日销售量y（千克）与每千克售价x（元）满足一次函数关系，其部分对应数据如下表所示：

每千克售价x/元

…

25

30

35

…

日销售量y/千克

…

110

100

90

…

(1)、该超市要获得1000元的日销售利润，每千克樱桃的售价应定为多少元？

(2)、该超市日销售利润能否达到2000元，若能，求出每千克樱桃的售价；若不能，请说明理由.

查看试题解析
27. 思考探索：

(1)、如图①在 $△ A B C$ 中， $A B = A C = 3$ ， $B C = 5$ ，点P为BC上一点，连接AP，若 $∠ A P C = 2 ∠ B$ ，则 $\frac{B P}{A B} =$ ；

(2)、在 $△ A B C$ 中， $∠ B = 30 °$ ，若 $∠ A P C = 2 ∠ B$ ，且AP把 $△ A B C$ 分成两个三角形，其中一个与 $△ A B C$ 相似，求 $∠ C$ 的度数；

(3)、如图②，在 $△ D E F$ 中， $D F = 6$ ， $E F = 9$ ， $∠ D Q F = 2 ∠ E$ ，点Q为EF上一点，点F关于直线DQ的对称点 $F^{'}$ 恰好落在线段DE上，求线段DE的长.

查看试题解析
28. 如图，已知 $∠ M O N = 90 °$ ，OT是 $∠ M O N$ 的平分线，A是射线OM上一点， $O A = 8 cm$ ，动点P从点A出发，以 $1cm / s$ 的速度沿AO水平向左作匀速运动，与此同时，动点Q从点O出发，也以 $1cm / s$ 的速度沿ON竖直向上作匀速运动.连接PQ，交OT于点B.经过O、P、Q三点作圆，交OT于点C，连接PC、QC.设运动时间为 $t (s)$ ，其中 $0 < t < 8$ .

(1)、求 $O P + O Q$ 的值；

(2)、是否存在实数t，使得线段OB的长度为 $2 \sqrt{2} cm$ ？若存在，求出t的值；若不存在，说明理由；

(3)、点P、Q在运动过程中，求证四边形OPCQ的面积是一定值.

查看试题解析

每千克售价x/元	…	25	30	35	…
日销售量y/千克	…	110	100	90	…