湖北省部分重点中学9 N新高考联盟2021-2022学年高三上学期数学新起点联考试卷

试卷更新日期：2021-09-24 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x (x - 2) < 0}$ ， $B = {x | - 1 < x < 1}$ ，则 $A \cap B =$ （）

A、 ${x | - 1 < x < 2}$ B、 ${x | 0 < x < 1}$ C、 ${x | x < - 1$ 或 $> 2}$ D、 ${x | x < 0$ 或 $> 1}$

查看试题解析
2. 若复数 $z$ 满足 $(1 + i) z = 3 - i$ （其中 $i$ 为虚数单位），则复数 $z$ 的共轭复数 $\bar{z} =$ （）

A、 $1 - 2 i$ B、 $1 + 2 i$ C、 $2 - 2 i$ D、 $2 + 2 i$

查看试题解析
3. 已知 $| \vec{a} | = 3 ， | \vec{b} | = 1 ， | \vec{a} - 2 \vec{b} | = \sqrt{19}$ ，则向量 $\vec{a} ， \vec{b}$ 的夹角为（）

A、 $30^{\circ}$ B、 $60^{\circ}$ C、 $120^{\circ}$ D、 $150^{\circ}$

查看试题解析
4. 设 $a = 3^{0.2} ， b = \log_{0.2} 3 ， c = \sin \frac{4 π}{5}$ ，则（）

A、 $b < a < c$ B、 $b < c < a$ C、 $a < b < c$ D、 $c < b < a$

查看试题解析
5. 已知函数 $f (x) = \sin (2 x + φ)$ 的部分图象如图所示，且经过点 $A (\frac{π}{4} ， \frac{\sqrt{3}}{2})$ ，则（）

A、 $f (x)$ 关于点 $(\frac{π}{3} ， 0)$ 对称 B、 $f (x)$ 关于直线 $x = \frac{π}{3}$ 对称 C、 $f (x + \frac{π}{12})$ 为奇函数 D、 $f (x + \frac{π}{6})$ 为偶函数

查看试题解析
6. 已知 $p$ ：“ $0 < a < 1$ ， $b > 1$ ”， $q$ ：“ $f (x) = a^{x} - b$ $(a > 0$ ，且 $a \neq 1)$ 的图象不过第一象限”，则 $p$ 是 $q$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右焦点为 $F_{1} ， F_{2}$ ，过 $F_{2}$ 的直线交双曲线右支于 $A ， B$ ，若 $\vec{B F_{1}} \cdot \vec{B F_{2}} = 0$ ，且 $\cos ∠ F_{1} A F_{2} = \frac{4}{5}$ ，则双曲线的离心率为（）

A、 $\sqrt{2}$ B、 $\frac{3}{2}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{\sqrt{10}}{2}$

查看试题解析
8. 定义空间直角坐标系中的任意点 $P (x ， y ， z)$ 的“ $N$ 数”为：在 $P$ 点的坐标中不同数字的个数，如： $N (1 ， 1 ， 1) = 1 ， N (1 ， 3 ， 1) = 2 ， N (1 ， 2 ， 3) = 3$ ，若点 $P$ 的坐标 $x ， y ， z$ $\in {0 ， 1 ， 2 ， 3}$ ，则所有这些点 $P$ 的“ $N$ 数”的平均值为（）

A、 $\frac{37}{16}$ B、64 C、 $\frac{25}{16}$ D、40

查看试题解析

二、多选题

9. 已知 $a > 0 ， b > 0 ， 2 a + b = 1$ ，则（）

A、 $\log_{0.5} a + \log_{0.5} b$ 的最大值为3 B、 $4^{a} + 2^{b}$ 的最小值为 $2 \sqrt{2}$ C、 $a \in (0 ， \frac{1}{2})$ D、 $a^{2} + 2 b^{2}$ 的最小值为 $\frac{1}{4}$

查看试题解析
10. 已知 $f (x)$ 为R上的偶函数，且 $f (x + 2)$ 是奇函数，则（）

A、 $f (x)$ 关于点 $(2 ， 0)$ 对称 B、 $f (x)$ 关于直线 $x = 2$ 对称 C、 $f (x)$ 的周期为4 D、 $f (x)$ 的周期为8

查看试题解析
11. 已知 $\vec{a} = (\sin α ， \cos 2 α + 5)$ ， $\vec{b} = (3 \sin α + 7 ， - 1)$ ，且 $\vec{a} ⊥ \vec{b}$ ，则（）

A、 $\sin α = \frac{3}{5}$ B、 $\sin 2 α = \frac{24}{25}$ C、 $\cos 2 α = \frac{7}{25}$ D、若 $- \frac{π}{2} < α < \frac{π}{2}$ ，则 $\tan (α + \frac{π}{4}) = 7$

查看试题解析
12. 如图，菱形 $A B C D$ 边长为 $2$ ， $∠ B A D = 60 °$ ， $E$ 为边 $A B$ 的中点．将 $△ A D E$ 沿 $D E$ 折起，使 $A$ 到 $A^{'}$ ，且平面 $A^{'} D E ⊥$ 平面 $B C D E$ ，连接 $A^{'} B$ ， $A^{'} C$ ．

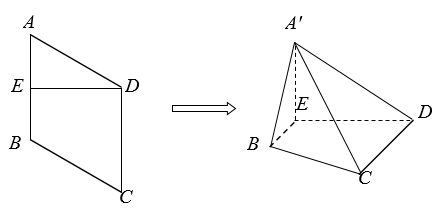
则下列结论中正确的是（）

A、 $B D ⊥ A^{'} C$ B、四面体 $A^{'} C D E$ 的外接球表面积为 $8 π$ C、 $B C$ 与 $A^{'} D$ 所成角的余弦值为 $\frac{3}{4}$ D、直线 $A^{'} B$ 与平面 $A^{'} C D$ 所成角的正弦值为 $\frac{\sqrt{6}}{4}$

查看试题解析

三、填空题

13. 海水稻的灌溉是将海水稀释后进行灌溉.某试验基地为了研究海水浓度 $x$ （‰）对亩产量 $y$ （吨）的影响，测得了某种海水稻的亩产量与海水浓度的数据如下表.绘制散点图发现，可用线性回归模型拟合亩产量 $y$ 与海水浓度 $x$ 之间的相关关系，最小二乘法计算得 $y$ 与 $x$ 之间的线性回归方程为 $\hat{y} = \hat{b} x + 0.88$ ，则 $\hat{b} =$

海水浓度 $x_{i}$ （‰）

3

4

5

6

7

亩产量 $y_{i}$ （吨）

0.52

0.48

0.39

0.3

0.21

查看试题解析
14. 直线 $l ： y = k x + 3$ $(k > 0)$ 与圆 $O ： x^{2} + y^{2} = 4$ 相交于 $A ， B$ ，若 $S_{Δ A O B} = \sqrt{3}$ ，则 $k =$ .

查看试题解析
15. 已知等比数列 ${a_{n}} ， {b_{n}}$ 的前 $n$ 项和分别记为 $S_{n} ， T_{n}$ ，且 $\frac{S_{n}}{T_{n}} = \frac{2^{n} + 1}{4}$ ，则 $\frac{a_{5}}{b_{5}} =$ .

查看试题解析
16. 点 $M$ 在函数 $y = 2 e^{x}$ 的图象上，若满足到直线 $y = 2 x + b$ 的距离为 $\sqrt{5}$ 的点 $M$ 只有 $2$ 个，则实数 $b$ 的取值范围为.

查看试题解析

四、解答题

17. 数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{1} = 1$ ， $a_{n + 1} = 2 S_{n} + 1$ ，等差数列 ${b_{n}}$ 的公差大于0.已知 $S_{2} = b_{2} + 1$ ，且 $b_{1} ， b_{2} ， b_{5}$ 成等比数列.

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、求数列 ${\frac{1}{b_{n} b_{n + 1}}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析

18. 从某企业生产的某种产品中抽取1000件，测量这些产品的一项质量指标值，由测量结果得如下频率分布表和频率分布直方图.

分组	频数	频率
[2.5，7.5)	2	0.002
[7.5，12.5)	m	0.054
[12.5，17.5)	106	0.106
[17.5，22.5)	149	0.149
[22.5，27.5)	352	n
[27.5，32.5)	190	0.190
[32.5，37.5)	100	0.100
[37.5，42.5)	47	0.047
合计	1000	1.000

(1)、求m，n，a的值；

(2)、求出这1000件产品质量指标值的样本平均数

\bar{x}

(同一组中的数据用该组区间的中点值作代表)；

(3)、由直方图可以认为，这种产品的质量指标值

Z

服从正态分布

N (μ ， σ^{2})

，其中

μ

近似为样本平均数

\bar{x}

，

σ^{2}

近似为样本方差

s^{2}

，其中已计算得

σ^{2} = 52.6

.如果产品的质量指标值位于区间

(10.50 ， 39.50)

，企业每件产品可以获利10元，如果产品的质量指标值位于区间

(10.50 ， 39.50)

之外，企业每件产品要损失100元，从该企业一天生产的产品中随机抽取20件产品，记

X

为抽取的20件产品所获得的总利润，求

E (X)

附： $\sqrt{52.6} \approx 7.25$ ， $P (μ - σ < x < μ + σ) = 0.6826$ ， $P (μ - 2 σ < x < μ + 2 σ) = 0.9544$ .

查看试题解析

19. 在 $△ A B C$ 中，角A ， B ， C所对的边为a ， b ， c ，且满足 $b^{2} - a^{2} = a c$ ，若 $A = \frac{π}{6} .$

(1)、求角B；

(2)、若周长为6，求 $△ A B C$ 的面积.

查看试题解析
20. 如图，在三棱锥 $F - A B C$ 与三棱锥 $F - E B C$ 拼接而成的五面体中， $E F ⊥$ 平面 $B C E$ ，平面 $A B C ⊥$ 平面 $B C E$ ， $△ A B C$ 是边长为 $4$ 的正三角形， $△ B C E$ 是直角三角形，且 $B C = E C$

(1)、求证： $E F / /$ 平面 $A B C$ ；

(2)、若多面体 $A B C E F$ 的体积为 $8 \sqrt{3}$ ，求直线 $A F$ 与平面 $B E F$ 所成角的正弦值.

查看试题解析
21. 已知 $A (2 ， \sqrt{2})$ 为椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 与抛物线 $y^{2} = 2 p x$ 的交点，设椭圆的左右焦点为 $F_{1} ， F_{2}$ ，抛物线的焦点为 $F$ ，直线 $A F$ 将 $△ A F_{1} F_{2}$ 的面积分为9：7两部分.

(1)、求椭圆及抛物线的方程；

(2)、若直线 $l$ ： $y = k x + m$ 与椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 相交于 $P 、 Q$ 两点，且 $△ O P Q$ 的重心恰好在圆 $O ： x^{2} + y^{2} = 1$ 上，求 $m$ 的取值范围.

查看试题解析
22. 已知 $f (x) = \ln x + a x$ （ $a \in R$ ）

(1)、讨论 $f (x)$ 的单调性；

(2)、当 $a = 1$ 时，若 $f (x) \leq k (x + 1) + b$ 在 $(0 ， + \infty)$ 上恒成立，证明： $\frac{2 k + b - 2}{k - 1}$ 的最小值为 $- e + 1$ .

查看试题解析

海水浓度 $x_{i}$ （‰）	3	4	5	6	7
亩产量 $y_{i}$ （吨）	0.52	0.48	0.39	0.3	0.21