河南省大联考2021-2022学年高三上学期理数阶段性测试试卷（一）

试卷更新日期：2021-09-24 类型：月考试卷

进入出卷网下载

一、单选题

1. 设全集 $U = {x | x \geq 0}$ ， $M = {x | x - x^{2} > 0}$ ， $N = {y | y = 2^{x} ， x \geq 0}$ ，则 $M \cap (∁_{U} N) =$ （）

A、 $[0 ， + \infty)$ B、 $(1 ， + \infty)$ C、 $[0 ， 1)$ D、 $(0 ， 1)$

查看试题解析
2. 复数 $z$ 满足 $(2 + i) z = \bar{z} - 4$ ，则 $\overline{z}$ =（）

A、 $3 + i$ B、 $- 3 - i$ C、 $- 1 + i$ D、 $- 1 - i$

查看试题解析
3. 已知命题 $p$ 是“若 $\tan α = 1$ ，则 $α = \frac{π}{4}$ ”的否命题，命题 $q$ 为“ $\exists x \in R$ ， $2^{x} < 0$ ”，则下列命题中，假命题是（）

A、 $p \lor q$ B、 $\neg p \land \neg q$ C、 $p \lor \neg q$ D、 $p \land \neg q$

查看试题解析
4. 已知非常数函数 $f (x)$ 满足 $f (- x) f (x) = 1$ $(x \in R)$ ，则下列函数中，不是奇函数的为（）

A、 $\frac{f (x) - 1}{f (x) + 1}$ B、 $\frac{f (x) + 1}{f (x) - 1}$ C、 $f (x) - \frac{1}{f (x)}$ D、 $f (x) + \frac{1}{f (x)}$

查看试题解析
5. 若向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = 1$ ， $| \vec{b} | = \sqrt{2}$ ， $(2 \vec{a} + \vec{b}) ⊥ \vec{b}$ ，则 $\vec{a}$ ， $\vec{b}$ 的夹角为（）

A、 $\frac{3 π}{4}$ B、 $\frac{2 π}{3}$ C、 $\frac{π}{3}$ D、 $\frac{π}{4}$

查看试题解析
6. 已知 $a > 0$ ，若 ${(x + \frac{9}{x^{2}})}^{6}$ 与 ${(x^{2} + \frac{a}{x})}^{6}$ 的展开式中的常数项相等，则 $a =$ （）

A、1 B、 $\sqrt{3}$ C、3 D、9

查看试题解析
7. 如图，圆锥的底面直径 $A B = 2$ ，其侧面展开图为半圆，底面圆的弦 $A D = \sqrt{3}$ ，则异面直线 $A D$ 与 $B C$ 所成的角的余弦值为（）

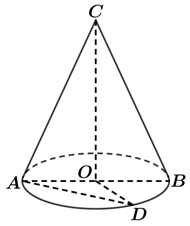A、0 B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{4}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
8. 已知函数 $f (x) = \sin (ω x + φ)$ （ $ω > 0$ ， $| φ | < \frac{π}{2}$ ）的最小正周期为 $π$ ，将其图象向左平移 $\frac{π}{3}$ 个单位长度后对应的函数为偶函数，则 $f (\frac{π}{6}) =$ （）

A、 $- \frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、1 D、 $\frac{1}{2}$

查看试题解析
9. 已知抛物线 $x^{2} = 4 y$ 的焦点为 $F$ ，过 $F$ 作一条直线与抛物线及抛物线的准线相交，交点从上到下依次为 $A$ ， $B$ ， $C$ ，若 $\frac{| B C |}{| B F |} = \sqrt{5}$ ，则 $| A B | =$ （）

A、3 B、4 C、5 D、6

查看试题解析
10. 若函数 $f (x) = \sin (\frac{π}{2} + x) \sin (x - 2 π) - a \cos (π - x)$ 在区间 $(0 ， \frac{π}{2}]$ 上单调递增，则实数 $a$ 的取值范围是（）

A、 $(- \infty ， - 1]$ B、 $(- \infty ， \sqrt{2}]$ C、 $(- \infty ， \sqrt{2}]$ D、 $[1 ， + \infty)$

查看试题解析
11. 一个三棱锥与一个四棱锥的正视图与侧视图均是如图所示的图形，则三棱锥与四棱锥的体积之比的最小值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
12. 已知函数 $f (x) = \frac{e^{x}}{e^{x} + 2 x}$ ，若实数 $m$ ， $n$ 满足 $e^{m + n} = 4 m n$ ，且 $f (m) = - \frac{1}{2}$ ，则 $f (n) =$ （）

A、 $\frac{3}{2}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $- \frac{1}{2}$

查看试题解析

二、填空题

13. 已知点 $P (x ， y)$ 满足约束条件 ${\begin{array}{l} x + y \geq 4 \\ x - y \geq 0 \\ x \leq 4 \end{array}$ ，则 $z = 2 x + y$ 的最小值为．

查看试题解析
14. 双曲线 $x^{2} - \frac{y^{2}}{m} = 1$ $(m > 0)$ 的离心率为2，则它的一个焦点到一条渐近线的距离为．

查看试题解析
15. 某专业资格考试包含甲、乙、丙 $3$ 个科目，假设小张甲科目合格的概率为 $\frac{3}{4}$ ，乙、丙科目合格的概率相等，且 $3$ 个科目是否合格相互独立．设小张 $3$ 科中合格的科目数为 $X$ ，若 $P (X = 3) = \frac{3}{16}$ ，则 $E (X) =$ ．

查看试题解析
16. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，若 $B = \frac{π}{3}$ ， $a + c = 6$ ，则 $A C$ 边上的中线长的取值范围是．

查看试题解析

三、解答题

17. 某职业培训学校现有六个专业，往年每年各专业的招生人数和就业率（直接就业的学生人数与招生人数的比值）统计如下表：

专业	机电维修	艺术舞蹈	汽车美容	餐饮	电脑技术	美容美发
招生人数	100	100	300	200	800	500
就业率	100%	70%	90%	80%	50%	80%

（Ⅰ）从该校往年的学生中随机抽取1人，求该生是“餐饮”专业且直接就业的概率；

（Ⅱ）为适应人才市场的需求，该校决定明年将“电脑技术”专业的招生人数减少 $m$ $(0 < m \leq 400)$ ，将“机电维修”专业的招生人数增加 $\frac{m}{3}$ ，假设“电脑技术”专业的直接就业人数不变，“机电维修”专业的就业率不变，其他专业的招生人数和就业率都不变，要使招生人数调整后全校整体的就业率比往年提高5个百分点，求 $m$ 的值．

查看试题解析

18. 已知在数列 ${a_{n}}$ 中， $a_{1} = 1$ ， $a_{2} = 3$ ，且当 $n \geq 2$ 时， $a_{n + 1} = 4 (a_{n} - a_{n - 1})$ ．
（Ⅰ）证明： ${a_{n + 1} - 2 a_{n}}$ 是等比数列；

（Ⅱ）求数列 ${a_{n}}$ 的通项公式．

查看试题解析
19. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $D$ 为棱 $A_{1} B_{1}$ 的中点．

（Ⅰ）证明： $A_{1} C //$ 平面 $B C_{1} D$ ；

（Ⅱ）若 $C_{1} D ⊥ A_{1} B_{1}$ ，且 $C_{1} D = \frac{1}{2} A_{1} B_{1}$ ， $A C = \sqrt{2}$ ， $A A_{1} = 1$ ，求二面角 $B - C D - C_{1}$ 的正弦值．

查看试题解析
20. 已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的上顶点 $A$ 与下顶点 $B$ 在直线 $l$ ： $x - 2 y + 1 = 0$ 的两侧，且点 $B$ 到 $l$ 的距离是 $A$ 到 $l$ 的距离的3倍．
（Ⅰ）求 $b$ 的值；

（Ⅱ）设 $C$ 与 $l$ 交于 $P$ ， $Q$ 两点，求证：直线 $B P$ 与 $B Q$ 的斜率之和为定值．

查看试题解析
21. 已知函数 $f (x) = \ln x + a x^{2} - (a + 2) x$ $(a \in R)$
（Ⅰ）若 $a = 0$ ，求曲线 $y = f (x)$ 在 $x = 1$ 处的切线方程；

（Ⅱ）若 $f (x)$ 存在极小值点 $t$ ，证明 $f (t) \leq - 2$ ．

查看试题解析
22. 在直角坐标系 $x O y$ 中，圆 $C$ 的圆心坐标为 $(2 ， 0)$ ，以坐标原点 $O$ 为极点， $x$ 轴正半轴为极轴建立极坐标系，点 $M$ 的极坐标为 $(\sqrt{3} ， \frac{π}{6})$ ，且过 $M$ 点只能作一条圆 $C$ 的切线．

(1)、求圆 $C$ 的极坐标方程；

(2)、直线 $θ = α$ （ $0 < α < \frac{π}{2}$ ， $ρ \in R$ ）和圆 $C$ 相交于两点 $A$ ， $B$ ，若 $\vec{O A} = \vec{A B}$ ，求 $\cos α$ ．

查看试题解析
23. 已知函数 $f (x) = | 2 x + 1 | - | x - a |$ $(a \in R)$ ．
（Ⅰ）若 $a = 1$ ，解不等式 $f (x) < 2$ ；

（Ⅱ）若 $f (x) > - 1$ 恒成立，求 $a$ 的取值范围．

查看试题解析