上海市金山区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 在下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、2. 下列关于 的方程中一定没有实数根的是( )A、 ; B、 ; C、 ; D、 .3. 下列函数中,函数值y随x的增大而增大的是( )A、 ; B、 ; C、 ; D、 .4. 已知三角形的面积一定,则它底边a上的高h与底边a之间的函数关系的图象大致是( )A、
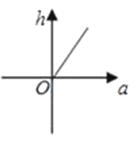 B、
B、 C、
C、 D、
D、 5. 下列四组数据为三角形的三边,其中能构成直角三角形的是( )A、 ; B、 ; C、 ; D、 .6. 下列命题中,是假命题的是( )A、两条直角边对应相等的两个直角三角形全等 ; B、每个命题都有逆命题; C、每个定理都有逆定理; D、在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.
5. 下列四组数据为三角形的三边,其中能构成直角三角形的是( )A、 ; B、 ; C、 ; D、 .6. 下列命题中,是假命题的是( )A、两条直角边对应相等的两个直角三角形全等 ; B、每个命题都有逆命题; C、每个定理都有逆定理; D、在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.二、填空题
-
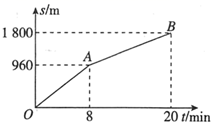
7. 化简: = .8. 方程 的根是 .9. 在实数范围内因式分解: .10. 函数 的定义域是 .11. 已知反比例函数 ( 是常数, )的图像有一支在第四象限,那么 的取值范围是 .12. 某工厂前年的产值为500万元,去年比前年的产值增加了 ,如果今年的产值估计比去年也增加了 ,那么该工厂今年的产值将是万元.13. 已知两点A、B,到这两点距离相等的点的轨迹是 .14. 小明从家步行到学校,图中的折线 反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图像提供的信息,线段 表示的函数解析式是 .
 15. 如果点A的坐标为 ,点B的坐标为 ,那么 两点的距离等于 .16. 如图,已知 中, ,点D在 上, ,点E为垂足,且 ,联结 ,则 的大小为 .
15. 如果点A的坐标为 ,点B的坐标为 ,那么 两点的距离等于 .16. 如图,已知 中, ,点D在 上, ,点E为垂足,且 ,联结 ,则 的大小为 .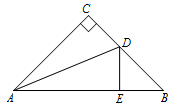 17. 《九章算术》中有一道题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”大致意思是:有一根长为10尺的竹子,中间折断后竹梢触底,如图,离开根部为3尺( ),那么折断后的竹子( )的高度为 .
17. 《九章算术》中有一道题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”大致意思是:有一根长为10尺的竹子,中间折断后竹梢触底,如图,离开根部为3尺( ),那么折断后的竹子( )的高度为 . 18. 已知,如图,在 中, 是 上的中线,如果将 沿 翻折后,点B的对应点 ,那么 的长为 .
18. 已知,如图,在 中, 是 上的中线,如果将 沿 翻折后,点B的对应点 ,那么 的长为 .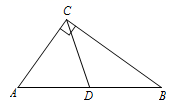
三、解答题
-
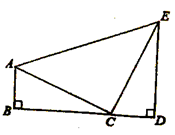
19. 计算: .20. 解方程: .21. 已知: , 与 成正比例, 与x成反比例.当 时, ;当 时, .求y与x的函数解析式.22. 如图, 、 分别垂直于 ,点 、 是垂足,且 , ,求证: 是直角三角形.
 23. 已知:如图, ,点A在 上, .
23. 已知:如图, ,点A在 上, .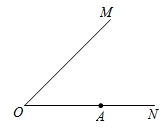 (1)、①求作线段 的垂直平分线,交 于点B;
(1)、①求作线段 的垂直平分线,交 于点B;②联结 ,求作 的角平分线 ;
(2)、根据①②的条件,求 的长.(第①、②题保留作图痕迹,不需要写出作图步骤)
24. 已知:如图, 中, 分别是 上的中线, 相交于点O,联结 .求证: (1)、 ;(2)、 垂直平分 .
(1)、 ;(2)、 垂直平分 .

