黑龙江省齐齐哈尔市碾子山区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 计算2x³ $\cdot$ x²的结果是（）

A、2x B、2x⁵ C、2x⁶ D、x⁵

查看试题解析
2. 下列图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 新冠病毒的直径最小大约为0.000 000 08米，将这个数字用科学记数法表示为（）

A、8 × 10 ^{- 8} B、8 × 10 ^{- 9} C、8 × 10 ^{- 7} D、0.8 × 10 ^{- 7}

查看试题解析
4. 下列计算正确的是（）

A、a²•a³=a⁶ B、（a+b）（a﹣2b）=a²﹣2b² C、（ab³）²=a²b⁶ D、5a﹣2a=3

查看试题解析
5. 根据下列已知条件，能唯一画出△ABC的是（　　）

A、AB=3，BC=4，AC=8 B、∠C=90°，AB=6 C、AB=3，BC=3，∠C=30° D、∠A=60°，∠B=45°，AB=4

查看试题解析
6. 已知一个正多边形的一个内角为150度，则它的边数为（）

A、12 B、8 C、9 D、7

查看试题解析
7. 若分式 $\frac{| x | - 2}{x + 2}$ 的值为零，则x的值是（）

A、2 B、-2 C、±2 D、1

查看试题解析
8. 王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚可以放进一个等腰直角三角板（AC=BC ，　∠ACB=90°）点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为（）

A、10cm B、14cm C、20cm D、6cm

查看试题解析
9. 小张和小王同时从学校出发去距离15千米的上海世博园，小张比小王每小时多行1千米，结果比小王早到半小时，设小王每小时走x千米，则（）

A、 $\frac{15}{x + 1} - \frac{15}{x} = \frac{1}{2}$ B、 $\frac{15}{x} - \frac{15}{x + 1} = \frac{1}{2}$ C、 $\frac{15}{x - 1} - \frac{15}{x} = \frac{1}{2}$ D、 $\frac{15}{x} - \frac{15}{x - 1} = \frac{1}{2}$

查看试题解析
10. 如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点．若 $A E = 2$ ，当 $E F + C F$ 取得最小值时，则 $∠ E C F$ 的度数为（）

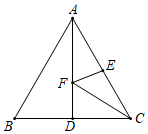A、15° B、225° C、30° D、45°

查看试题解析

二、填空题

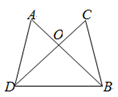
11. 当x＝时，分式 $\frac{1}{x - 3}$ 无意义．

查看试题解析
12. 三角形的两边长分别是2cm和5cm，第三边也是整数，则第三边的长可能是.

查看试题解析
13. 如图，AB，CD相交于点O，AD＝CB，请你补充一个条件，使得△AOD ≌△COB．你补充的条件是．

查看试题解析
14. 已知M（a ， 3）和N（4，b）关于x轴对称，则a= ， b= ．

查看试题解析
15. 已知等腰三角形的两边长分别为x和y，且x和y满足|x﹣3|+(y﹣1)²=0，则这个等腰三角形的周长为．

查看试题解析
16. 因式分解： $x^{2} y - 4 y$ = ．

查看试题解析
17. 如图，△ABC中，∠C=90°，∠BAC的平分线交BC于点D ，若CD=3，则点D到AB的距离是．

查看试题解析
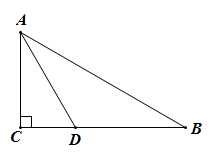18. 如图，在△ABC中，AB=AC=11，∠BAC=120°，AD是△ABC的中线，AE是∠BAD的角平分线，DF∥AB交AE的延长线于点F，则DF的长为．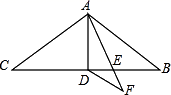

查看试题解析

三、解答题

19. 计算：

(1)、 ${(2 x^{3} y)}^{2} \cdot \frac{1}{2} x y$ ；

(2)、 $\sqrt{16} + {(2 - \sqrt{2})}^{0} - {(\frac{1}{2})}^{- 2} + | - 1 |$ ；

(3)、 $\frac{a - 1}{a^{2} - 4 a + 4} \div \frac{a^{2} - 1}{a^{2} - 4}$

查看试题解析
20. 解方程：

(1)、 $\frac{7}{x - 2} = \frac{5}{x}$

(2)、 $\frac{2 - x}{x - 3} + \frac{1}{3 - x} = 1$

查看试题解析
21. 先化简分式：（1﹣ $\frac{x}{x - 1}$ ）÷ $\frac{x + 1}{x^{2} - x}$ ，然后在﹣2，﹣1，0，1，2中选一个你认为合适的x的值，代入求值．

查看试题解析
22. 已知：如图，已知△ABC ，

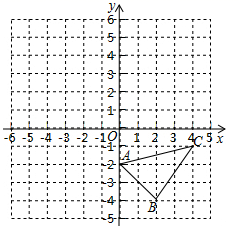
⑴分别画出与△ABC关于x轴、y轴对称的图形△A₁B₁C₁和△A₂B₂C₂；

⑵写出△A₁B₁C₁和△A₂B₂C₂各顶点坐标．

查看试题解析
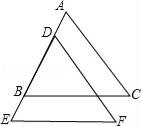
23. 如图，AC=DF，AD=BE，BC=EF．
求证：∠C=∠F．

查看试题解析
24. 在预防新型冠状病毒性肺炎期间，市民对医用口罩的需求越来越大，某药店第一次用30000元购进口罩若干个，第二次又用30000元购进该款口罩．但第二次每个口罩的进价是第一次进价的1.25倍，购进的数量比第一次少了2000个，

(1)、求第一次和第二次分别购进医用口罩多少个？

(2)、药店第一次购进口罩后，先以每个4元价格出售，由于第二批同款口罩进价提高了，药店又将第二批口罩提升至4.5元出售，由于当地医院医疗物资紧张，药店将两次销售口罩的收入全部捐给了医院购买医疗物资，问该药店捐款多少元？

查看试题解析
25. 如图△ABC是等边三角形，P是△ABC的角平分线BD上的一点，PE⊥AB于点E ，线段BP的垂直平分线交BC于点F ，垂足为Q ．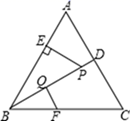

(1)、若BQ=2，求PE的长；

(2)、连接PF ， EF ，试判断△EFP的形状，并说明理由．

查看试题解析