黑龙江省齐齐哈尔市建华区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是 $($ 　　 $)$

A、 $a + a = a^{2}$ B、 $a \cdot a^{2} = a^{2}$ C、 ${(2 a)}^{2} = 2 a^{2}$ D、 $a + 2 a = 3 a$

查看试题解析
2. 下列标志中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列多项式乘法，能用平方差公式进行计算的是（）

A、 $(x + y) (-x-y)$ B、( $(2x + 3y) (2x-3z)$ C、 $(-a-b) (a-b)$ ) D、 $(m-n) (n-m)$

查看试题解析
4. 在△ABC中， ∠C=∠B，与△ABC全等的三角形有一个角是100°，那么△ABC中与这个角对应的角是（）

A、∠B B、∠A C、∠C D、∠B或∠C

查看试题解析
5. 如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S_△_ABC＝4cm² ，则S_阴影等于…（）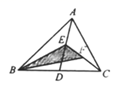

A、2cm² B、1cm² C、 $\frac{1}{2}$ cm² D、 $\frac{1}{4}$ cm²

查看试题解析
6. 如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形的形状是（）

A、锐角三角形； B、直角三角形； C、钝角三角形； D、等腰三角形．

查看试题解析
7. 不改变分式 $\frac{0.5 x - 1}{0.3 x + 2}$ 的值，把它的分子和分母中的各项的系数都化为整数，则所得结果为（）

A、 $\frac{5 x - 10}{3 x + 20}$ B、 $\frac{5 x - 1}{3 x + 2}$ C、 $\frac{2 x - 1}{3 x + 2}$ D、 $\frac{x - 2}{3 x + 20}$

查看试题解析
8. 下列四个说法：
①等腰三角形的腰一定大于其腰上的高；

②等腰三角形的两腰上的中线长相等；

③等腰三角形的高、中线、角平分线互相重合；

④等腰三角形的一边为5，另一边为10，则它的周长为20或25

其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，在△ABC中，D、E分别是AC、AB上的点，BD与CE相交于点O，给出四个条件：①OB=OC；②∠EBO=∠DCO；③∠BEO=∠CDO；④BE=CD．上述四个条件中，选择两个可以判定△ABC是等腰三角形的方法有（　　）

A、2种 B、3种 C、4种 D、6种

查看试题解析
10. 某学校学生进行急行军训练，预计行60千米的路程在下午5时到达，后来由于把速度加快20%，结果于下午4时到达，求原计划行军的速度．设原计划行军的速度为xkm/h ，则可列方程（　　）

A、 $\frac{60}{x} = \frac{60}{x + 20 %} + 1$ B、 $\frac{60}{x} = \frac{60}{x + 20 %} - 1$ C、 $\frac{60}{x} = \frac{60}{x (1 + 20 %)} + 1$ D、 $\frac{60}{x} = \frac{60}{x (1 + 20 %)} - 1$

查看试题解析

二、填空题

11. 纳米构建的世界是神奇而宏大的，21世纪，信息科学技术、生命科学技术和纳米科学技术是科学技术发展的主流．纳米是长度单位的一种，1纳米等于十亿分之一米，即1纳米＝0.000000001米，将数字0.000000001科学记数法可表示为．

查看试题解析
12. 当x时，分式 $\frac{1}{x^{2} - 4}$ 有意义．

查看试题解析
13. 如图，点E、F在BC上，AB=DC，∠B=∠C，请补充一个条件：，使△ABF≌△DCE．

查看试题解析
14. 计算 $a^{- 2} b^{3} \div {(a^{2} b)}^{- 3}$ =.

查看试题解析
15. 已知P是 $∠ A O B (∠ A O B < 90 °)$ 平分线上一点，点C在射线OA上，且 $∠ O C P = 135 °$ ，点D在射线OB上运动．若 $D P = C P$ ，则 $∠ O D P =$ ．

查看试题解析
16. 如图，已知 $∠ A O B = 30 °$ ，P是 $∠ A O B$ 内部的一个定点，点E．F分别是OA．OB上的动点，若 $△ P E F$ 周长的最小值为3，则 $O P =$ ．

查看试题解析
17. 如图， $△ A B C$ 中，AH为BC边上的高，记 $S_{△ A B C}$ 为S，AH的垂直平分线交边AB于点 $B_{1}$ ，交边AC于点 $A_{1}$ ，连接 $A_{1} B$ ，得到第一个三角形 $△ A_{1} B C$ ，作 $△ A_{1} B C$ 边BC上的高 $A_{1} H_{1}$ ；作高 $A_{1} H_{1}$ 的垂直平分线交边AB于点 $B_{2}$ ，交边AC于点 $A_{2}$ ，连接 $A_{2} B$ ，得到第二个三角形 $△ A_{2} B C$ ，作 $△ A_{2} B C$ 边BC上的高 $A_{2} H_{2}$ ；……依次这样作下去，则第2020个三角形 $△ A_{2020} B C$ 的面积为．

查看试题解析

三、解答题

18. 计算

(1)、 $x^{4 m + 1} \cdot x^{3 - m}$ ；

(2)、 ${(- 2 x^{3})}^{2} \cdot {(x y^{2})}^{3}$ ；

(3)、 $- 4 x^{2} (3 x - 2)$ ；

(4)、 $(3 x - 2 y) (3 x + 2 y) + {(2 x - y)}^{2} - 4 (3 x^{2} - x y)$ ．

查看试题解析
19. 分解因式

(1)、 $3 a (x - y) - 2 b (y - x)$ ；

(2)、 $4 a b^{2} - 4 b^{3} - a^{2} b$ ．

查看试题解析
20. 如图所示，在平面直角坐标系中，已知正方形ABCD的四个顶点坐标分别为： $A (0 ， 3)$ 、 $B (2 ， 4)$ 、 $C (3 ， 2)$ 、 $D (1 ， 1)$ ，将正方形ABCD沿y轴对折得到正方形 $A_{1} B_{1} C_{1} D_{1}$ ．

(1)、在图中作出正方形ABCD关于y轴的对称图形正方形 $A_{1} B_{1} C_{1} D_{1}$ ；

(2)、请你直接写出点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 、 $D_{1}$ 的坐标；

(3)、计算四边形 $B_{1} B D D_{1}$ 的面积为．

查看试题解析
21. 先化简再求值： $\frac{a^{2} - b^{2}}{a^{2} b - a b^{2}} \div (1 + \frac{a^{2} + b^{2}}{2 a b})$ ，其中 $a = - 2$ ， $b = 1$ ．

查看试题解析
22. 如图， $△ A B C$ 和 $△ A D E$ 都是等腰直角三角形， $∠ B A C = ∠ D A E = 90 °$ ，连结BD．CE交于点G．请你判断线段BD与线段CE的关系，并说明理由．

查看试题解析
23. A、B两地距80千米，一辆公共汽车从A地去B地，15分钟后又从A地同方向开出一辆小汽车去B地，小汽车车速是公共汽车车速的2倍，结果小汽车比公共汽车早33分钟到达B地，求两车速度．

查看试题解析
24. 阅读下面文字并填空：
数学习题课上李老师出了这样一道题：“如图1，在 $△ A B C$ 中，AD平分 $∠ B A C$ ， $∠ B = 2 ∠ C$ ．求证： $A B + B D = A C$ ．

李老师给出了如下简要分析：“要证 $A B + B D = A C$ 就是要证线段的和差问题，所以有两个方法，

(1)、
方法一：‘截长法’如图2，在AC上截取 $A E = A B$ ，连接DE，只要证 $B D =$ 即可，这就将证明线段和差问题为证明线段相等问题，只要证出 $△$ $≌ △$ ，得出 $∠ B = ∠ A E D$ 及 $B D =$ ，再证出 $∠$ $= ∠$ ，进而得出 $E D = E C$ ，则结论成立．此种证法的基础是‘已知AD平分 $∠ B A C$ ，将 $△ A B D$ 沿直线AD对折，使点B落在AC边上的点E处’成为可能．

(2)、
方法二：“补短法”如图3，延长AB至点F，使 $B F = B D$ ．只要证 $A F = A C$ 即可．此时先证 $∠$ $= ∠ C$ ，再证出 $△$ $≌ △$ ，则结论成立．”

查看试题解析