黑龙江省佳木斯市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列代数式中： $\frac{x}{2} ， \frac{1}{x} ， \frac{x}{π}$ ， $\frac{x^{2} - y^{2}}{x + y}$ ， $\frac{1}{2} x - y ， \frac{3 x + y}{5}$ ， $\frac{x^{2} - 2 x + 1}{x^{2} + 2 x}$ ，是分式的有（）

A、 $4$ 个 B、 $3$ 个 C、 $2$ 个 D、 $1$ 个

查看试题解析
2. 下列倡导节约的图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（）

A、 $3 cm$ ， $4 cm$ ， $8 cm$ B、 $8 cm$ ， $7 cm$ ， $15 cm$ C、 $5 cm$ ， $5 cm$ ， $11 cm$ D、 $12 cm$ ， $12 cm$ ， $20 cm$

查看试题解析
4. 下列计算正确的是（）

A、 $2 a + a = 3 a^{2}$ B、 ${(- 2 a)}^{3} = - 8 a^{3}$ C、 ${(a^{2})}^{3} \div a^{5} = 1$ D、 $3 a^{3} \cdot 2 a^{2} = 6 a^{6}$

查看试题解析
5. 若分式 $\frac{3 m^{2}}{2 m + n}$ 中的m，n同时扩大2倍，则该分式的值（）

A、不变 B、缩小到原来的 $\frac{1}{2}$ C、扩大2倍 D、扩大4倍

查看试题解析
6. 正多边形的每个内角都是144°，则它的边数是（）

A、10 B、13 C、15 D、19

查看试题解析
7. 已知 $4 x^{2} + m x y + 9 y^{2}$ 是完全平方式，则m的值为（）

A、 $- 6$ B、 $\pm 6$ C、 $12$ D、 $\pm 12$

查看试题解析
8. 如图，OP平分∠AOB，PC⊥OA于点C，点D在OB上，PC＝3，则PD的取值范围是（）

A、PD≥3 B、PD＞3 C、PD≤3 D、不能确定

查看试题解析
9. 某食堂购买了一批大米和面粉．已知购买大米的袋数是面粉袋数的2倍，购买大米共用了1800元，购买面粉共用了750元，每袋大米比每袋面粉的售价多10元．如果设购买面粉x袋，那么根据题意，下列方程中正确的是（　　）

A、 $\frac{1800}{2 x} = \frac{750}{x} - 10$ B、 $\frac{1800}{x} = \frac{750}{2 x} + 10$ C、 $\frac{1800}{2 x} = \frac{750}{x} + 10$ D、 $\frac{1800}{x} = \frac{750}{2 x} - 10$

查看试题解析
10. 在∆ABC和∆DEF中，其中∠C=∠F ，则下列条件①AC=DF ， ∠A=∠D；②AC=DF ， BC=EF；③∠A=∠D ， ∠B=∠E；④AB=DE ， ∠B=∠E；⑤AC=DF ， AB=DE ．其中能够判定这两个三角形全等的是（）

A、①②④ B、①②⑤ C、②③④ D、③④⑤

查看试题解析

二、填空题

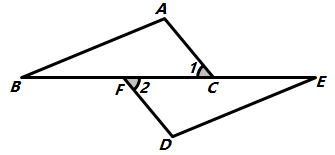
11. PM2.5是指大气中直径小于或等于0.00025cm的颗粒物，将0.00025用科学记数法表示为．

查看试题解析
12. 当 $x =$ 时，分式 $\frac{7}{4 - x^{2}}$ 没有意义．

查看试题解析
13. 如图，点B、F、C、E在同一直线上， $∠ 1 = ∠ 2$ ， $BF = EC$ ，要使 $△ ABC ≅ △ DEF$ ，还需添加的一个条件是（只需写出一个即可）.

查看试题解析
14. 当x时， ${(2 x - 4)}^{0} = 1$ .

查看试题解析
15. 如图，DE 是 ∆ABC 的边AB 的垂直平分线，点D 为垂足，DE 交AC 于点E ，且AC=8，BC=5，则∆BEC 的周长是．

查看试题解析
16. 若等腰三角形的一边5，一边等于6，则它的周长等于．

查看试题解析
17. 若一个多项式与 $- 2 x^{2}$ 的积为 $- 2 x^{5} + 4 x^{3} - x^{2}$ ，则这个多项式为．

查看试题解析
18. 在△ABC中，∠A= $\frac{1}{2}$ ∠B= $\frac{1}{3}$ ∠C，则∠B=度．

查看试题解析
19. 如图Rt△ABC中，∠C＝90°，∠A＝30°，BD是∠ABC的平分线，若BD＝10，则AC＝．

查看试题解析
20. 观察下列算式：①1×3-2²=3-4=-1 ；②2×4-3²=8-9=-1 ；③ 3×5-4²=15-16=-1，④4×6-5²=24-25=-1，⋯ ．⋯ ．按这个规律，第n 个式子应表示为． (用含n的式子表示)

查看试题解析

三、解答题

21. 先化简，再求值： $(\frac{a + 2}{a^{2} - 2 a} + \frac{1 - a}{a^{2} - 4 a + 4}) \div \frac{a - 4}{a}$ ，并从 $0 < a < 4$ 中选取合适的整数代入求值．

查看试题解析
22. 分解因式

(1)、 $x^{3} - 16 x$ ；

(2)、 $4 x - 4 x^{2} - 1$ ．

查看试题解析
23.

(1)、计算： $[x (x^{2} y^{2} - x y) - y (x^{2} - x^{2} y)] \div x^{2} y$ ．

(2)、解分式方程： $\frac{x - 3}{x + 3} - \frac{x + 3}{x - 3} = \frac{36}{x^{2} - 9}$ ．

查看试题解析
24. 如图所示，在平面直角坐标系中，A（﹣1，5）、B（﹣1，0）、C（﹣4，3）．

(1)、求出△ABC的面积；

(2)、在图形中作出△ABC关于y轴的对称图形△A₁B₁C₁ ．

查看试题解析
25. 已知a、b、c为 $△ A B C$ 的三边，且 ${(a - 1)}^{2} + {(b - 1)}^{2} + c^{2} = 2 c - 1$ ，试判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
26. 为了尽快实施“脱贫致富奔小康”宏伟意图，某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗，已知一棵苹果树苗比一棵梨树苗贵2元，购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元．

(1)、若两种树苗购买的棵数一样多，求梨树苗的单价；

(2)、若两种树苗共购买1100棵，且购买两种树苗的总费用不超过6000元，根据（1）中两种树苗的单价，求梨树苗至少购买多少棵．

查看试题解析
27. 如图，直线 AB 与 x 轴、y 轴分别交于点A、点B ，OA：OB：AB=3：4：5，且线段 OA 是方程 $\frac{2}{x + 3} = \frac{1}{x}$ 的解， M 是线段 OB 上一点，若将 ∆ABM 沿直线AM 折叠，点B 恰好落在x 轴上的点P 处．

(1)、求点 P 的坐标；

(2)、在y 轴上是否存在点 N ，使 ∆APN 是以PN 为底的等腰三角形？若存在，请直接写出点N 的坐标，若不存在，请说明理由．

查看试题解析
28. 如图①， $△ A C B$ 和 $△ D C E$ 均为等边三角形，点A ， D，E在一条直线上，连接 $B E$ ．

(1)、求证： $A D = B E$ ．

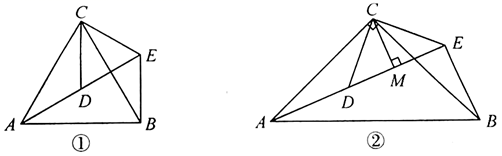(2)、求 $∠ A E B$ 的度数．

(3)、拓展探究：如图②， $△ A C B$ 和 $△ D C E$ 均为等腰直角三角形， $∠ A C B = ∠ D C E = 90 °$ ，点A ， D，E在一条直线上， $C M$ 为 $△ D C E$ 的边 $D E$ 上的高，连接 $B E$ ．
① $∠ A E B$ 的度数为；

②探索线段 $C M$ ， $A E$ ， $B E$ 之间的数量关系为．

查看试题解析