黑龙江省鸡西密山市（五四学制）2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列四个交通标志图中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在 $\frac{a - b}{2}$ ， $\frac{x (x + 3)}{x}$ ， $\frac{5 + x}{π}$ ， $\frac{a + b}{a - b}$ ，a＋ $\frac{1}{m}$ 中，是分式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 若等腰三角形的两条边长分别是3厘米和7厘米，则这个三角形的周长为（　　）

A、13厘米 B、17厘米 C、13厘米或17厘米 D、以上结论均不对

查看试题解析
4. 下列结论：
①横坐标为 $- 3$ 的点在经过点 $(- 3 ， 0)$ 且平行于y轴的直线上；

② $m \neq 0$ 时，点 $P (m^{2} ， - m)$ 在第四象限；

③点 $(- 3 ， 4)$ 关于y轴对称的点的坐标是 $(- 3 ， - 4)$ ；

④在第一象限的点N到x轴的距离是1，到y轴的距离是2，则点N的坐标为 $(2 ， 1)$ ．

其中正确的是（）．

A、①③ B、②④ C、①④ D、②③

查看试题解析
5. 如果多项式y²﹣4my+4是完全平方式，那么m的值是（　　）

A、1 B、﹣1 C、±1 D、±2

查看试题解析
6. 下列等式从左到右的变形是因式分解的是（）

A、2x（x+3）＝2x²+6x B、x²﹣y²＝（x+y）（x﹣y） C、x²+2xy+y²+1＝（x+y）²+1 D、24xy²＝3x•8y²

查看试题解析
7. 若关于x的方程 $\frac{x + m}{x - 3}$ + $\frac{3 m}{3 - x}$ =3的解为正数，则m的取值范围是（　　）

A、m＜ $\frac{9}{2}$ B、m＜ $\frac{9}{2}$ 且m≠ $\frac{3}{2}$ C、m＞﹣ $\frac{9}{4}$ D、m＞﹣ $\frac{9}{4}$ 且m≠﹣ $\frac{3}{4}$

查看试题解析
8. 已知实数x，y，m满足 $\sqrt{x + 2} + | 3x + y + m | = 0$ ，且y为负数，则m的取值范围是（）

A、m＞6 B、m＜6 C、m＞﹣6 D、m＜﹣6

查看试题解析
9. 如图，在△ABC中，AB=AC ， ∠A=36°，BD ， CE分别平分∠ABC ， ∠ACB ，若CD=3，则CE等于（　　）

A、2 B、2.5 C、3 D、3.5

查看试题解析
10. 如图，△ABC是等边三角形，AQ=PQ ， PR⊥AB于点R ， PS⊥AC于点S ， PR=PS.下列结论：①点P在∠A的角平分线上；②AS=AR；③QP∥AR；④△BRP≌△QSP ．其中，正确的有（）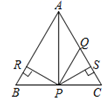

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 在① $\sqrt{14}$ ；② $\sqrt{a^{2} + b^{2}}$ ；③ $\sqrt{27}$ ；④ $\sqrt{m^{2} + 1}$ 中，最简二次根式有个．

查看试题解析
12. 知xy＝﹣3，x+y＝2，则代数式x²y+xy²的值是．

查看试题解析
13. 已知4×2^a×2^a⁺¹＝2⁹ ，且2a+b＝8，求a^b＝．

查看试题解析
14. 已知m²﹣n²＝16，m+n＝6，则m﹣n＝．

查看试题解析
15. 已知点A（x，－4）与点B（3，y）关于y轴对称，那么x＋y的值为．

查看试题解析
16. 如图已知∠B=∠C，请同学从这①BE=CE，②AB=DC，③∠BAE=∠CDE三个等式中再选出一个作为条件，可以推出△AED是等腰三角形的有（填序号）．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A B ＝ A C$ ，点D在 $A C$ 上，且 $B D ＝ B C ＝ A D$ ，则 $∠ A ＝$ 度．

查看试题解析
18. 如图，在△ABC中，直线ED是线段BC的垂直平分线，直线ED分别交BC、AB于点D、点E ，已知BD=3，△ABC的周长为20，则△AEC的周长为

查看试题解析
19. 如图，在锐角三角形ABC中，AC＝6，△ABC的面积为15，∠BAC的平分线交BC于点D ， M ， N分别是AD和AB上的动点，则BM+MN的最小值是．

查看试题解析
20. 如图，∠AOB=60°，OC平分∠AOB，如果射线OA上的点E满足△OCE是等腰三角形，那么∠OEC的度数为

查看试题解析

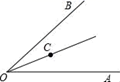
三、解答题

21. 计算题：

(1)、 $(\sqrt{24} - \sqrt{\frac{1}{2}}) - (\sqrt{\frac{1}{8}} + \sqrt{6})$

(2)、（2a） $^{3}$ ·b $^{4}$ ÷8a $^{3}$ b $^{2}$

(3)、（- $\frac{a}{b}$ ） $^{2}$ ·（- $\frac{b^{2}}{2 a}$ ） $^{3}$ ÷（-ab $^{4}$ ）

(4)、（4 $\sqrt{2}$ +6 $\sqrt{6}$ ）÷2 $\sqrt{2}$

(5)、1- $\frac{a - b}{a + 2 b} \div \frac{a^{2} - b^{2}}{a^{2} + 4 a b + 4 b^{2}}$

(6)、（x-y+ $\frac{4 x y}{x - y}$ ）（x+y- $\frac{4 x y}{x + y}$ ）

查看试题解析
22. 解方程

(1)、 $\frac{3}{x^{2} + 2 x} - \frac{1}{x^{2} - 2 x} = 0$

(2)、 $\frac{3}{2} - \frac{1}{3 x-1} = \frac{5}{6 x - 2}$

(3)、 $\frac{5 x + 2}{x^{2} + x} = \frac{3}{x + 1}$

(4)、 $\frac{5}{2 x - 5} = \frac{2}{2 x + 5}$

查看试题解析
23. 分解因式

(1)、 $(a - b) (x - y) - (b - a) (x + y)$

(2)、4+12（x-y）+9（x-y） $^{^{2}}$

(3)、 $6 x y^{2} - 9 x^{2} y - y^{3}$

(4)、 ${(2 a - b)}^{2} + 8 a b$

查看试题解析
24. 先化简，再求值： $\frac{x^{2} - 1}{x^{2} - 2 x + 1}$ ÷ $\frac{x + 1}{x - 1} \cdot \frac{1 - x}{1 + x}$ ，其中x＝ $\frac{1}{2}$ ．

查看试题解析
25. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．

⑴请画出△ABC关于x轴成轴对称的图形△A₁B₁C₁ ，并写出A₁、B₁、C₁的坐标；

⑵在y轴上找一点P，使PA+PB的值最小，请画出点P的位置．

查看试题解析
26. 如图，在△ABC中，AB边的垂直平分线l₁交BC于点D ， AC边的垂直平分线l₂交BC于点E ， l₁与l₂相交于点O ，连接OB ， OC ，若△ADE的周长为6 cm ， △OBC的周长为16 cm ．

(1)、求线段BC的长；

(2)、连接OA ，求线段OA的长；

(3)、若∠BAC＝120°，求∠DAE的度数．

查看试题解析
27. 应用题（步骤要完整）

(1)、一辆汽车开往距离出发地180km的目的地，出发后第一小时内按原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前40min到达目的地．求前一小时的行驶速度．

(2)、两个工程队共同参与一项筑路工程，甲队单独施工1个月完成总工程 $\frac{1}{3}$ ，这时增加了乙队，两队又共同工作了半个月，总工程全部完成．哪个队的施工快？

查看试题解析
28. 如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形AOB，点C为x正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边△CBD，连接DA并延长，交y轴于点E．

(1)、△OBC与△ABD全等吗？判断并证明你的结论；

(2)、当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？

查看试题解析