黑龙江省鹤岗市绥滨县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式：① $\frac{1}{a}$ ，② $\frac{x}{1 + π}$ ，③ $\frac{x - 1}{5}$ ，④ $\frac{2}{2 x + y}$ ，其中是分式的有（）

A、①②③④ B、①④ C、①②④ D、②④

查看试题解析
2. 下列运算正确的是（）．

A、a· $a^{2} {=a}^{2}$ B、 ${(a^{5})}^{3} {=a}^{8}$ C、 ${(ab)}^{3} {=a}^{3} b^{3}$ D、 $a^{6}$ ÷ $a^{2}$ = $a^{3}$

查看试题解析
3. 下列是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列长度的三条线段，哪一组不能构成三角形（）

A、3，3，3 B、3，4，5 C、5，6，10 D、4，5，9

查看试题解析
5. 若点P（ $m$ ，3）与点Q（1， $n$ ）关于y轴对称，则（）

A、 $m = - 1, n = - 3$ B、 $m = 1, n = 3$ C、 $m = - 1, n = 3$ D、 $m = 1, n = - 3$

查看试题解析
6. 下列运用平方差公式计算，错误的是（）

A、（a+b）（a﹣b）=a²﹣b² B、（2x+1）（2x﹣1）=2x²﹣1 C、（x+1）（x﹣1）=x²﹣1 D、（﹣3x+2）（﹣3x﹣2）=9x²﹣4

查看试题解析
7. 直角三角形两直角边长分别是30cm和40cm，则斜边上的中线长为（）

A、15 cm B、20 cm C、25 cm D、50 cm

查看试题解析
8. 随着5G网络技术的发展，市场对5G产品的需求越来越大，为满足市场需求，某大型5G产品生产厂家更新技术后，加快了生产速度，现在平均每天比更新技术前多生产30万件产品，现在生产500万件产品所需的时间与更新技术前生产400万件产品所需时间相同，设更新技术前每天生产x万件，依据题意得（）

A、 $\frac{400}{x - 30} = \frac{500}{x}$ B、 $\frac{400}{x} = \frac{500}{x + 30}$ C、 $\frac{400}{x} = \frac{500}{x - 30}$ D、 $\frac{400}{x + 30} = \frac{500}{x}$

查看试题解析
9. 如图，在△ABC中，AC的垂直平分线分别交AC、BC于E，D两点，EC＝4，△ABC的周长为23，则△ABD的周长为（）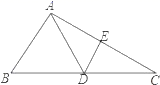

A、13 B、15 C、17 D、19

查看试题解析
10. 如图，BF=EC，∠B=∠E，请问添加下面哪个条件不能判断△ABC≌△DEF（　）

A、AC=DF B、AB=ED C、DF∥AC D、∠A=∠D

查看试题解析

二、填空题

11. 等腰三角形的一个底角为 $50 °$ ，则它的顶角的度数为．

查看试题解析
12. 2020年11月1日0点至11月11日24时“天猫双11”成交额共计人民币4982亿元，用科学记数法表示为元．

查看试题解析
13. 已知 $x + y = 4$ ， $x y = 3$ ，则 $x^{2} + y^{2}$ 的值为．

查看试题解析
14. 当x时，分式 $\frac{1}{x - 5}$ 有意义；当x时，分式 $\frac{x^{2} - 1}{x + 1}$ 的值为零

查看试题解析
15. 已知单项式 $3 x^{2} y^{3}$ 与 $- 5 x^{2} y^{2}$ 的积为 $m x^{4} y^{n}$ ，那么m-n= ．

查看试题解析
16. 如图，AB⊥BD于点B，ED⊥BD于点D，AB＝CD，BC＝DE，则∠ACE＝．

查看试题解析
17. 一个长方形的面积为 $x^{2} - 2 x y + x$ ，长是 $x$ ，则这个长方形的宽是．

查看试题解析
18. 一个正多边形的外角与它相邻的内角之比为1：4，那么这个多边形的边数为．

查看试题解析
19. 如图，∠ACB=90°，AC=BC，BE⊥CE，AD⊥CE于D点，AD=2.5cm，DE=1.7cm，则BE的长为.

查看试题解析
20. 古希腊数学家把1、3、6、10、15、21……叫做三角形数，其中1是共有一个三角形数，3是共有3个三角形数，6是共有6个三角形数…… 依次类推，那么第七个图共有三角数是，第n个图形共有三角形数是．

查看试题解析

三、解答题

21. 计算

(1)、3(y-z)²-(2y+z)· $(- z + 2 y)$ ；

(2)、 $[x y (3 x - 2) - y (x^{2} - 2 x)] \div x^{2} y$ ．

查看试题解析
22. 将下列各式因式分解：

(1)、x²-9y²；

(2)、3ax²+6axy＋3ay² ．

查看试题解析
23. 解下列分式方程：

(1)、 $\frac{2}{x - 5} = \frac{3}{x}$ ；

(2)、 $\frac{2}{3 x - 1} - 1 = \frac{3}{6 x - 2}$ ．

查看试题解析
24. 先化简，再求值： $(\frac{x^{2} - 4 x + 4}{x^{2} - 4} - \frac{x}{x + 2}) \div \frac{x - 1}{x + 2}$ ，其中 $x = - 3$ .

查看试题解析
25. 在平面直角坐标系中，每个小正方形的边长为1，点A的坐标为（-3，2）．请按要求分别完成下列各小题：

(1)、画出△ABC关于Y轴对称的△ $A_{1} B_{1} C_{1}$ ，则点 $A_{1}$ 的坐标是；

(2)、△ABC的面积是．

(3)、在x轴上找到一点P ，使得PA+PA₁最短，画出图形并求出P点坐标．

查看试题解析
26. 如图，点E在CD上，BC与AE交于点F ， AB=CB ， BE=BD ， ∠1=∠2．

求证：∠2=∠3．

查看试题解析
27. 某商店购进 $A$ 、 $B$ 两种商品，购买1个 $A$ 商品比购买1个 $B$ 商品多花10元，并且花费300元购买 $A$ 商品和花费100元购买 $B$ 商品的数量相等．

(1)、求购买一个 $A$ 商品和一个 $B$ 商品各需要多少元；

(2)、商店准备购买 $A$ 、 $B$ 两种商品共80个，若 $A$ 商品的数量不少于 $B$ 商品数量的4倍，并且购买 $A$ 、 $B$ 商品的总费用不低于1000元且不高于1050元，那么商店有哪几种购买方案？

查看试题解析
28. 如图，在等边三角形ABC的顶点A、C处各有一只蜗牛，它们同时出发，以相同的速度分别由A向B、由C向A爬行，经过t分钟后，它们分别爬行到了D、E处．设在爬行过程中DC与BE的交点为F ．

(1)、当点D、E不是AB、AC的中点时，图中有全等三角形吗？如果没有，请说明理由；如果有，请找出所有的全等三角形，并选择其中一对进行证明．

(2)、问蜗牛在爬行过程中DC与BE所成的∠BFC的大小有无变化？请证明你的结论．

查看试题解析