黑龙江省哈尔滨市五常市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 如图， $△ A B C$ 是等边三角形，AD是角平分线， $△ A D E$ 是等边三角形，下列结论错误的是（）

A、 $A D ⊥ B C$ B、 $E F = F D$ C、 $B E = B D$ D、 $A E = A C$

查看试题解析
2. 点 $M (3 ， 4)$ 关于x轴对称的点的坐标为（）

A、 $(3 ， - 4)$ B、 $(- 3 ， - 4)$ C、 $(- 3 ， 4)$ D、 $(- 3 ， 2)$

查看试题解析
3. 下列运算正确的是（）．

A、 $a^{2} + 2 a = 3 a^{3}$ B、 ${(- 2 a^{3})}^{2} = 4 a^{5}$ C、 $(a + 2) (a - 1) = a^{2} + a - 2$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
4. 下列运算中，错误的是（）

A、 $\frac{a}{b} = \frac{a c}{b c} (c \neq 0)$ B、 $\frac{- a - b}{a + b} = - 1$ C、 $\frac{0.5 a + b}{0.2 a - 0.3 b} = \frac{5 a + 10 b}{2 a - 3 b}$ D、 $\frac{x - y}{x + y} = \frac{y - x}{y + x}$

查看试题解析
5. 下列图形中不是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
6. 下列各组线段中，能组成三角形的是（）

A、4，5，10 B、7，6，8 C、3.3，1.2，1.1 D、4，2，6

查看试题解析
7. 如图，在下列图形中，最具有稳定性的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，已知∠ABC＝∠BAD ，再添加一个条件，仍不能判定△ABC≌△BAD的是（　　）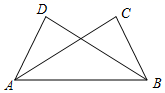

A、AC＝BD B、∠C＝∠D C、AD＝BC D、∠ABD＝∠BAC

查看试题解析
9. 到三角形三边的距离相等的点是（）

A、三角形三内角平分线的交点； B、三角形三边中线的交点； C、三角形三边高的交点； D、三角形三边中垂线的交点。

查看试题解析
10. 如图，A，B两点在正方形网格的格点上，每个方格都是边长为1的正方形，点C也在格点上，且△ABC为等腰三角形，满足条件的点C有（）

A、6个 B、7个 C、8个 D、9个

查看试题解析

二、填空题

11. 人体中红细胞的直径约为0.0000077 m，数据0.0000077用科学记数法表示为

查看试题解析
12. 从一个多边形的一个顶点出发，一共可作9条对角线，则这个多边形的内角和是度．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，AD平分 $∠ B A C$ ，交BC边于点D ，若 $A B = 12$ ， $C D = 4$ ，则 $△ A B D$ 的面积为．

查看试题解析
14. 当 $s = t + \frac{1}{2}$ 时，代数式 $s^{2} - 2 s t + t^{2}$ 的值为．

查看试题解析
15. 分式方程 $\frac{1}{2 x} = \frac{1}{x + 1}$ 的解为．

查看试题解析
16. 因式分解： $x^{3} ﹣ 2 x^{2} y + x y^{2} =$ ．

查看试题解析
17. 计算： $(16 x^{3} - 8 x^{2} + 4 x) \div (- 2 x) =$ ．

查看试题解析
18. 一个三角形的周长为偶数，其中两条边长分别为6和2019，则满足上述条件的三角形有个．

查看试题解析
19. 已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40^o ，则此等腰三角形的顶角度数为

查看试题解析
20. 已知 $x + y = 5 ， x y = 6$ ，则 $x^{2} + y^{2}$ 的值等于．

查看试题解析

三、解答题

21. 计算

(1)、 $2 {(a^{4})}^{3} + {(a^{3})}^{2} {(a^{2})}^{3} - a^{2} \cdot a^{10}$

(2)、 ${(3 x - 2 y)}^{2} + (2 x + 3 y) (2 x - 3 y)$

查看试题解析
22. △ABC在平面直角坐标系中的位置如图所示．A、B、C三点在格点上．

⑴作出△ABC关于y轴对称的△A₁B₁C₁ ，并写出点C₁的坐标；

⑵在y轴上找点D，使得AD+BD最小，直接写出点D的坐标．

查看试题解析
23. 先化简，再求值：
$(\frac{a + 2}{a^{2} - 2 a} - \frac{a - 1}{a^{2} - 4 a + 4}) \div \frac{a - 4}{a}$ ，其中 $a = 4 - 3^{0}$ ．

查看试题解析
24. 已知：如图，点D、E在 $△ ABC$ 的边BC上， $A D = A E$ ， $B D = C E$ ．求证：

(1)、 $A B = A C$ ；

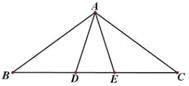(2)、若 $∠ BAC = 108^{°}$ ， $∠ DAE = 36^{°}$ ，直接写出图中除 $△ ABC$ 与 $△ ADE$ 外所有的等腰三角形．

查看试题解析
25. “六·一”儿童节前，某玩具商店根据市场调查，用2500元购进一批儿童玩
具，上市后很快脱销，接着又用4500元购进第二批这种玩具，所购数量是第一批数量的1.5

倍，但每套进价多了10元．

(1)、求第一批玩具每套的进价是多少元？

(2)、如果这两批玩具每套售价相同，且全部售完后总利润不低于25%，那么每套售价至少是多少元？

查看试题解析
26. 已知在四边形ABCD中， $∠ A = ∠ C = 90 °$ ．

(1)、如图1，若BE平分 $∠ A B C$ ，DF平分 $∠ A D C$ 的邻补角，请写出BE与DF的位置关系并证明；

(2)、如图2，若BF、DE分别平分 $∠ A B C$ 、 $∠ A D C$ 的邻补角，判断DE与BF位置关系并证明；

(3)、如图3，若BE、DE分别五等分 $∠ A B C$ 、 $∠ A D C$ 的邻补角（即 $∠ C D E = \frac{1}{5} ∠ C D N ， ∠ C B E = \frac{1}{5} ∠ C B M$ ），求 $∠ E$ 度数．

查看试题解析
27. 如图， $△ A B D$ 和 $△ B C E$ 都是等边三角形，AE与CD相交于F ，连接BF ．

(1)、求证： $A E = C D$ ；

(2)、求证：BF平分 $∠ D F E$ ．

查看试题解析