黑龙江省哈尔滨市通河县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 下列长度的三条线段能组成三角形的是( )A、1cm,2cm,3cm B、2cm,3cm,5.5cm C、5cm,8cm,12cm D、4cm,5cm,9cm2. 下列四个图形中,是轴对称图形的有( )
 A、4个 B、3个 C、2个 D、1个3. 如图, , ,垂足分别为点 ,点 , 、 相交于点O , ,则图中全等三角形共有( )
A、4个 B、3个 C、2个 D、1个3. 如图, , ,垂足分别为点 ,点 , 、 相交于点O , ,则图中全等三角形共有( ) A、2对 B、3对 C、4对 D、5对4. 一个多边形内角和是1440°,则这个多边形的边数为( )A、7 B、8 C、9 D、105. 如图是作 的作图痕迹,则此作图的已知条件是( )
A、2对 B、3对 C、4对 D、5对4. 一个多边形内角和是1440°,则这个多边形的边数为( )A、7 B、8 C、9 D、105. 如图是作 的作图痕迹,则此作图的已知条件是( )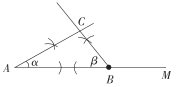 A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角6. 在△ABC中,∠A∶∠B∶∠C=1∶4∶5,则△ABC是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、等腰三角形7. 若 ,则 的值是( )A、6 B、5 C、9 D、88. 下列各式能利用完全平方公式分解因式的是( )A、 B、 C、 D、9. 已知xy=﹣3,x+y=2,则代数式x2y+xy2的值是( )A、﹣6 B、6 C、﹣5 D、﹣110. 如图所示,在 中, , 是 的角平分线, , ,垂足分别为E、F,① , ;② ;③若点P为 上任意一点,且 ,则 的取值范围是 ;④ .其中,正确的个数是( )
A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角6. 在△ABC中,∠A∶∠B∶∠C=1∶4∶5,则△ABC是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、等腰三角形7. 若 ,则 的值是( )A、6 B、5 C、9 D、88. 下列各式能利用完全平方公式分解因式的是( )A、 B、 C、 D、9. 已知xy=﹣3,x+y=2,则代数式x2y+xy2的值是( )A、﹣6 B、6 C、﹣5 D、﹣110. 如图所示,在 中, , 是 的角平分线, , ,垂足分别为E、F,① , ;② ;③若点P为 上任意一点,且 ,则 的取值范围是 ;④ .其中,正确的个数是( )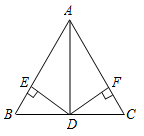 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 点P(2,-3)关于x轴对称的点P′的坐标是 .12. 分解因式: .13. 计算: .14. 已知如图, ,请你添加一个适当的条件 , 使 .(只添一个)
 15. 若分式 的值为负数,则x的取值范围是 .16. 如图,已知在△ABC中,AB=AC , AB的垂直平分线分别交AC于点D , 交AB于点E . 若∠DBC=18°,则∠A=°.
15. 若分式 的值为负数,则x的取值范围是 .16. 如图,已知在△ABC中,AB=AC , AB的垂直平分线分别交AC于点D , 交AB于点E . 若∠DBC=18°,则∠A=°. 17. 在 中,a,b,c分别是 , , 的对边,且 , ,若三边长为连续整数,则 .18. 等腰三角形底角为15°,其腰长为8,则此三角面积为 .19. 在Rt ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,已知CD=2,那么BD= .20. 如图所示, 为 中线,D为 中点, , ,连接 , .若 的面积为3,则 的面积为 .
17. 在 中,a,b,c分别是 , , 的对边,且 , ,若三边长为连续整数,则 .18. 等腰三角形底角为15°,其腰长为8,则此三角面积为 .19. 在Rt ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,已知CD=2,那么BD= .20. 如图所示, 为 中线,D为 中点, , ,连接 , .若 的面积为3,则 的面积为 .
三、解答题
-
21. 先化简,再求值: ,其中 .22. 在正方形网格中,建立如图所示的平面直角坐标系, 的三个顶点都在格点上, 关于y轴对称图形为 .(要求:A与 ,B与 ,C与 相对应)
 (1)、写出 的坐标,并画出 的图形;(2)、求 的面积.23. 解答.(1)、(2)、24. 已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N.(1)、如图1,求证:AE=BD;
(1)、写出 的坐标,并画出 的图形;(2)、求 的面积.23. 解答.(1)、(2)、24. 已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N.(1)、如图1,求证:AE=BD; (2)、如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.
(2)、如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.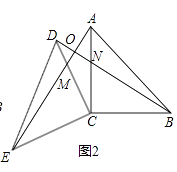 25. 服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.(1)、求每件羽绒服的标价是多少元;(2)、进入12月份,该服装店决定把剩余的羽绒服按10月份标价的八折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?26. 如图所示, 是 的高,点H为 的垂直平分线与 的交点, .(1)、如图1,求证: ;
25. 服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.(1)、求每件羽绒服的标价是多少元;(2)、进入12月份,该服装店决定把剩余的羽绒服按10月份标价的八折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?26. 如图所示, 是 的高,点H为 的垂直平分线与 的交点, .(1)、如图1,求证: ; (2)、如图2,若 ,求证: ;
(2)、如图2,若 ,求证: ; (3)、在(2)的条件下,若 , ,求 的长.
(3)、在(2)的条件下,若 , ,求 的长. 27. 我们在第十二章《全等三角形》中学习了全等三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题.例如:我们在解决:“如图1,在 中, , ,线段 经过点C , 且 于点D , 于点E . 求证: , ”这个问题时,只要证明 ,即可得到解决,
27. 我们在第十二章《全等三角形》中学习了全等三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题.例如:我们在解决:“如图1,在 中, , ,线段 经过点C , 且 于点D , 于点E . 求证: , ”这个问题时,只要证明 ,即可得到解决,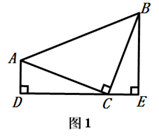
积累经验:
(1)、请写出证明过程;(2)、如图2,在平面直角坐标系中, 中, , ,点A的坐标为 ,点C的坐标为 ,求点B与x轴的距离.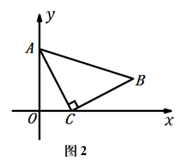 (3)、如图3, 在平面直角坐标系中, , ,点A的坐标为 ,点C的坐标为 ,求点B的坐标.
(3)、如图3, 在平面直角坐标系中, , ,点A的坐标为 ,点C的坐标为 ,求点B的坐标.