黑龙江省哈尔滨市巴彦县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $\frac{x^{2}}{y}$ ， $\frac{a b^{2}}{5 π}$ ， $\frac{3 x y}{10}$ ， $\frac{m + n}{m}$ ， $\frac{b - c}{5 + a}$ 中，分式有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列图形中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $- a^{2} b^{3} \cdot 3 a b^{3} = - 3 a^{2} b^{5}$ C、 ${(x - y)}^{6} = - {(y - x)}^{6}$ D、 ${(a^{3} b)}^{2} = a^{6} b^{2}$

查看试题解析
4. 若 $x^{2} - k x + 16$ 是一个整式的平方，则k的值（）

A、8 B、-8 C、4 D、8或-8

查看试题解析
5. 到三角形三个顶点距离相等的点是（）的交点．

A、三角形三边垂直平分线的交点 B、三角形三条高的交点 C、三角形三条中线的交点 D、三角形三条角平分线的交点

查看试题解析
6. 点 $M (- 5 ， 3)$ 关于x轴的对称点的坐标是（）

A、 $(- 5 ， - 3)$ B、 $(5 ， - 3)$ C、 $(5 ， 3)$ D、 $(- 5 ， 3)$

查看试题解析
7. 等腰三角形有两条边的长为4cm和9cm，则该三角形的周长（）

A、17cm B、22cm C、17cm和22cm D、18cm

查看试题解析
8. 如图， $△ A B C$ 中， $B E$ 是角平分线， $D E / / B C$ 交 $A B$ 于D，交 $A C$ 于E，若 $D E = 7$ ， $A D = 5$ ，则 $A B =$ （）

A、10 B、12 C、14 D、16

查看试题解析
9. 如图，已知△ABC中，AB=AC，AD=AE，∠BAE=30°，则∠DEC等于（）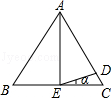

A、7.5° B、10° C、15° D、18°

查看试题解析
10. 下列说法中正确的个数有（）
①关于某直线对称的两个三角形是全等三角形

②全等三角形是关于某直线对称的

③两个图形关于某直线对称，则这两个图形一定分别位于这条直线的两侧

④有一条公共边的两个全等三角形关于公共边所在的直线对称

⑤轴对称图形的对应点所连线段被对称轴垂直平分

⑥等腰三角形的角平分线，中线，高线互相重合

A、2 B、3 C、4 D、5个

查看试题解析

二、填空题

11. 当x时，分式 $\frac{x - 1}{2 x + 1}$ 有意义．

查看试题解析
12. 在 $△ A B C$ 中， $A B = A C = 6$ ， $∠ A = 30 °$ ，则 $△ A B C$ 的面积等于．

查看试题解析
13. 若 $a^{m} = 5$ ， $a^{n} = 6$ ，则 $a^{m + 2 n}$ 的值为．

查看试题解析
14. 分解因式： $a x^{2} - 2 a^{2} x + a^{3} =$ ．

查看试题解析
15. 若 $m - \frac{1}{m} = 1$ ，则 $m^{2} + \frac{1}{m^{2}} =$ ．

查看试题解析
16. 方程 $\frac{x}{x - 1} = \frac{3}{2 x - 2} - 2$ 的解是.

查看试题解析
17. 如图 $∠ E A F = 15 °$ ， $A B = B C = C D = D E = E F$ ，则 $∠ D E F =$ ．

查看试题解析
18. 如图， $D E$ 是 $△ A B C$ 中 $A C$ 边的垂直平分线，若 $B C = 6 cm$ ， $A B = 8 cm$ ，则 $△ E B C$ 的周长为．

查看试题解析
19. 在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 80 °$ ，点D在直线 $B C$ 上， $C D = C A$ ，则 $∠ B A D$ 的度数为．

查看试题解析
20. 如图，在等边 $△ A B C$ 中，点D在 $B C$ 边延长线上，连接 $A D$ ，点E在线段 $A D$ 上，连接 $B E$ ，交线段 $A C$ 于点F， $A E = B C$ ， $\frac{A D}{C D} = \frac{7}{3}$ ， $B D - C F = \frac{14}{3}$ ，则线段 $A F$ 的长度为．

查看试题解析

三、解答题

21. 计算

(1)、 $(3 x + 2) (3 x - 2) - {(3 x - 1)}^{2}$

(2)、 $(2 x - y + 3) (2 x + y - 3)$

查看试题解析
22. 先化简，再求值： $(\frac{a + 2}{a^{2} - 2 a} - \frac{a - 1}{a^{2} - 4 a + 4}) \div \frac{a - 4}{a}$ ，其中 $a = {(π + 1)}^{0} + 5$ ．

查看试题解析
23. 如图

(1)、①作出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ．
②通过画图在x轴上找出点P，使得 $P A$ 与 $P C$ 之和最小．

(2)、连接 $P C_{1}$ 、 $O C_{1}$ 、 $O P$ ，则 $△ P O C_{1}$ 的面积为．

查看试题解析
24. 已知： $△ A C B$ 和 $△ D C E$ 都是等腰直角三角形， $∠ A C B = ∠ D C E = 90 °$ ，连接 $A D$ 、 $B E$ 交于点H， $A D$ 与 $E C$ 交于点G， $B E$ 与 $A C$ 交于点F．

(1)、如图1，求证： $A D = B E$ ；

(2)、如图2，若 $A C = D C$ ，在不添加任何辅助线的情况下，请直接写出图2中四对全等的直角三角形．

查看试题解析
25. 和兴商厦销售A，B两种商品，售出1件A种商品和4件B种商品所得利润为600元，售出3件A种商品和5件B种商品所得利润为1100元．

(1)、求每件A种商品和每件B种商品售出后所得利润分别为多少元？

(2)、由于需求量大，A、B两种商品很快售完，和兴商厦决定再一次购进A、B两种商品共30件，如果将这30件商品全部售完后所得利润高于4000元，那么和兴商厦至少需要购进多少件A种商品？

查看试题解析
26. 在 $△ A B C$ 中，点D、E在 $A B$ 边上，满足 $A C = A E$ ， $B C = B D$ ，且 $∠ D C E = 45 °$ ．

(1)、如图1，求证： $∠ A + ∠ B = 90 °$ ；

(2)、如图2，过点E作 $E F ⊥ C D$ 交 $C D$ 于点G，交 $A C$ 于点F，求证： $C F = E D$ ．

查看试题解析
27. 如图，在 $△ A B C$ 中，点A，点B在x轴上， $∠ A C B = 90 °$ ， $C A = C B$ ， $B C$ 交y轴于点D，点D的坐标为 $(0 ， 1)$ ，点C的横坐标为-3．

(1)、如图1，求点C的纵坐标．

(2)、如图2，点E在线段 $B C$ 上，点E横坐标为t， $△ A B E$ 的面积为S，求S与t的关系式（不要求写出t的取值范围）

(3)、如图3，在（2）的条件下，延长 $A E$ 交y轴于点G，点F在 $E G$ 的延长线上，连接 $B F$ ， $G H$ 平分 $∠ A G O$ 交x轴于点H， $∠ A F B = 45 °$ ， $C A = F B$ ，求H点的坐标．

查看试题解析