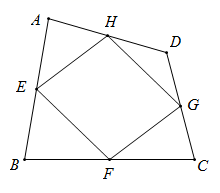
黑龙江省大庆市肇源县(五四学制)2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 若 ,则下列式子错误的是( )A、 B、 C、 D、2. 等腰三角形是轴对称图形,它的对称轴是( )A、中线 B、底边上的中线 C、中线所在的直线 D、底边上的中线所在的直线3. 如图,在 中, 的垂直平分线交 于点D, 平分 ,若 ,则 的度数为( )
 A、 B、 C、 D、4. 若关于x的方程 有增根,则k的值为( ).
A、 B、 C、 D、4. 若关于x的方程 有增根,则k的值为( ).
A、3 B、1 C、0 D、-15. 若0<m<1, 则m、m2、 的大小关系是( )A、m<m2< B、m2<m< C、<m<m2 D、<m2<m6. 某商品的进价是500元,标价是750元,商店要求以利润率为5%的售价打折出售,售货员可以打几折出售此商品( )A、5 B、6 C、7 D、87. 如图, 中, ,将 绕点A按顺时针方向旋转 ,得到 ,则 的度数为( ) A、 B、 C、 D、8. 甲、乙两地之间的高速公路全长200千米,比原来国道的长度减少了20千米.高速公路通车后,某长途汽车的行驶速度提高了45千米/时,从甲地到乙地的行驶时间缩短了一半.设该长途汽车在原来国道上行驶的速度为x千米/时,根据题意,下列方程正确的是( )A、 B、 C、 D、9. 一个正多边形的内角和等于1080°,这个正多边形的每个外角是( )A、30° B、45° C、60° D、75°10. 关于 的不等式组 ,有四个整数解,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、8. 甲、乙两地之间的高速公路全长200千米,比原来国道的长度减少了20千米.高速公路通车后,某长途汽车的行驶速度提高了45千米/时,从甲地到乙地的行驶时间缩短了一半.设该长途汽车在原来国道上行驶的速度为x千米/时,根据题意,下列方程正确的是( )A、 B、 C、 D、9. 一个正多边形的内角和等于1080°,这个正多边形的每个外角是( )A、30° B、45° C、60° D、75°10. 关于 的不等式组 ,有四个整数解,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 如图,点P是∠AOB平分线OC上一点,PD⊥OB , 垂足为D , 若PD=2,则点P到边OA的距离是 .
 12. 一个正多边形的内角和是外角和的3倍,则这个正多边形的一个内角的度数是度.13. 某校组织开展了“诗词大会”的知识竞赛初赛,共有 20 道题. 答对一题加 10 分,答错 或不答一题扣 5 分,小辉在初赛得分超过 160 分顺利进入决赛. 设他答对 x 道题,根据题意,可列出关于 x 的不等式为 .14. 如果若分式 的值为0,则实数a的值为.15. 一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示,则关于x的不等式ax+b≥kx的解集为 .
12. 一个正多边形的内角和是外角和的3倍,则这个正多边形的一个内角的度数是度.13. 某校组织开展了“诗词大会”的知识竞赛初赛,共有 20 道题. 答对一题加 10 分,答错 或不答一题扣 5 分,小辉在初赛得分超过 160 分顺利进入决赛. 设他答对 x 道题,根据题意,可列出关于 x 的不等式为 .14. 如果若分式 的值为0,则实数a的值为.15. 一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示,则关于x的不等式ax+b≥kx的解集为 . 16. 如图,在四边形 中,点P是对角线 的中点,点E、F分别是 、 的中点, , ,则 的度数是 .
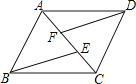
16. 如图,在四边形 中,点P是对角线 的中点,点E、F分别是 、 的中点, , ,则 的度数是 . 17. 如图,平行四边形ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB丁点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列四个结论:①∠ACD=30°;② ;③ =AC·AD;④OE:OA=1: 其中结论正确的序号是 . (把所有正确结论的序号都选上)
17. 如图,平行四边形ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB丁点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列四个结论:①∠ACD=30°;② ;③ =AC·AD;④OE:OA=1: 其中结论正确的序号是 . (把所有正确结论的序号都选上)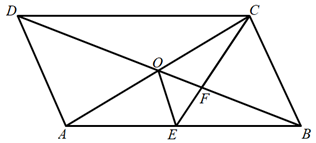 18. 如图,在平行四边形ABCD中,按以下步骤作图:
18. 如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB , AD于点M , N;
②分别以M , N为圆心,以大于 MN的长为半径作弧,两弧相交于点P;
③作AP射线,交边CD于点Q .
若QC=1,BC=3,则平行四边形ABCD周长为

三、解答题
-
19. 解方程:20. 化简并求值:(1- )÷ ,其中x= -121. 因式分解:(1)、 ;(2)、 .22.
如图,在▱ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
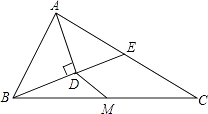
 23. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
23. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).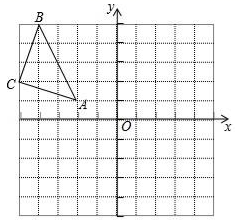 (1)、画出△ABC关于原点O成中心对称的△A1B1C1;(2)、写出△A1B1C1的顶点坐标;(3)、求出△A1B1C1的面积.24. 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB.
(1)、画出△ABC关于原点O成中心对称的△A1B1C1;(2)、写出△A1B1C1的顶点坐标;(3)、求出△A1B1C1的面积.24. 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB. (1)、求点P与点Q之间的距离;(2)、求∠APB的度数.25. 已知:如图, ,EF垂直平分 ,与 , , 分别交于点E,F,O.
(1)、求点P与点Q之间的距离;(2)、求∠APB的度数.25. 已知:如图, ,EF垂直平分 ,与 , , 分别交于点E,F,O.求证:
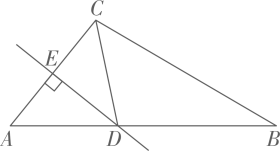
 (1)、 ≌ ;(2)、 .26. 如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC,求证:BD=DF.
(1)、 ≌ ;(2)、 .26. 如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC,求证:BD=DF.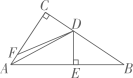 27. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?
27. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?